A block of mass 2 kg is having velocity 4√5ms−1 in the positive x - direction at the origin. The only force acting on it is F=(3x2−12x)N. Its velocity when it is at x=2 m is
(a)8ms−1
(b)4ms−1
(c)10√24ms−1
(d)20ms−1
The correct Answer is:A
To solve the problem step by step, we will use the work-energy principle and the relationship between force, mass, and acceleration.
Step 1: Identify the given values
- Mass of the block, m=2kg
- Initial velocity, v0=4√5m/s
- Force acting on the block, F=3x2−12xN
- Position where we need to find the velocity, x=2m
Step 2: Write down the force equation
From Newton's second law, we know:
F=ma
where a is the acceleration. We can express acceleration in terms of velocity v and position x:
a=dvdt=dvdx⋅v
Thus, we can rewrite the force equation as:
F=m⋅v⋅dvdx
Step 3: Substitute the force into the equation
Substituting the expression for force into the equation gives:
3x2−12x=2vdvdx
Step 4: Rearranging and integrating
Rearranging the equation, we have:
3x2−12x2=vdvdx
Now, we can separate variables:
∫vdv=∫3x2−12x2dx
Step 5: Integrate both sides
Integrating the left side:
∫vdv=v22+C
Integrating the right side:
∫3x2−12x2dx=32⋅x33−122⋅x22=x32−3x2
Step 6: Set up the limits for integration
We will evaluate from x=0 to x=2:
(v22)vv0=(x32−3x2)20
Step 7: Calculate the right side
Calculating the right side:
- At x=2:
232−3(22)=82−3(4)=4−12=−8
- At x=0:
032−3(02)=0
Thus, the right side evaluates to:
−8−0=−8
Step 8: Set up the equation
Now we have:
v22−(4√5)22=−8
Calculating (4√5)2=80:
v22−802=−8
This simplifies to:
v22−40=−8
Thus:
v22=32
Multiplying both sides by 2 gives:
v2=64
Step 9: Solve for velocity
Taking the square root:
v=√64=8m/s
Final Answer
The velocity of the block when it is at x=2m is 8m/s.
---
- Mass of the block, m=2kg
- Initial velocity, v0=4√5m/s
- Force acting on the block, F=3x2−12xN
- Position where we need to find the velocity, x=2m
From Newton's second law, we know:
F=ma
where a is the acceleration. We can express acceleration in terms of velocity v and position x:
a=dvdt=dvdx⋅v
Thus, we can rewrite the force equation as:
F=m⋅v⋅dvdx
Substituting the expression for force into the equation gives:
3x2−12x=2vdvdx
Rearranging the equation, we have:
3x2−12x2=vdvdx
Now, we can separate variables:
∫vdv=∫3x2−12x2dx
Integrating the left side:
∫vdv=v22+C
Integrating the right side:
∫3x2−12x2dx=32⋅x33−122⋅x22=x32−3x2
We will evaluate from x=0 to x=2:
(v22)vv0=(x32−3x2)20
Calculating the right side:
- At x=2:
232−3(22)=82−3(4)=4−12=−8
- At x=0:
032−3(02)=0
Thus, the right side evaluates to:
−8−0=−8
Now we have:
v22−(4√5)22=−8
Calculating (4√5)2=80:
v22−802=−8
This simplifies to:
v22−40=−8
Thus:
v22=32
Multiplying both sides by 2 gives:
v2=64
Taking the square root:
v=√64=8m/s
The velocity of the block when it is at x=2m is 8m/s.
Similar Questions
A block of mass 2 kg is kept at origin at t = 0 and is having velocity 4√5m/s in positive x - direction. The only force on it is a conservative and its potential energy is defined as U=−x3+6x2+15 (SI units). Its velocity when the force acting on it is minimum (after the time t = 0 ) is
View SolutionA block of mass 2 kg is moving with a velocity of 2ˆi−ˆj+3ˆk m/s. Find the magnitude and direction of momentum of the block with the x-axis.
View SolutionA body of mass 2kg is moving along positive X - direction with a velocity of 5ms−1 Now a force of 10√2 N N is applied at an angle 45° with X - axis. Its velocity after 3s is,
View SolutionA body of mass 1 kg is moving with velocity 30ms−1 due north. It is acted on by a force of 10 N due east for 4 seconds. Find the velocity of the body after the force ceases to act.
View SolutionA particle A of mass 10/7kg is moving in the positive direction of x−aξs. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)

View SolutionA particle A of mass 10/7kg is moving in the positive direction of x-axis. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)

View SolutionA ball of mass 0.5 kg is moving with a velocity of 2ms−1. It if subjected to a force of x Newton for 2s. Because of this force, the ball moves with a velocity of 3ms−1 . The value of x is :
View SolutionA particle of mass 10−2kg is moving along the positive x axis under the influence of a force F(x)=−K/(2x2) where K=10−2Nm2. At time t=0 it is at x=1.0m and its velocity is v=0.
(a) Find its velocity when it reaches x=0.50m.
(b) Find the time at which it reaches x=0.25m.
View SolutionA block of the mass of 1 kg is moving on the x-axis . A force F acting on the block is shown . The velocity of the block at time t = 2 s is - 3ms−1 what is the speed of the block at time t = 4 s?
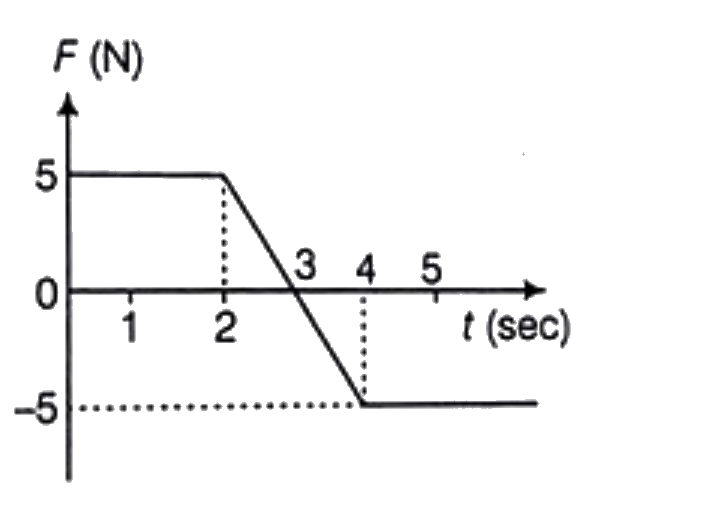
View SolutionThe block shown in the diagram has a mass of 2μg and a charge of 2×10−9C. If the block is given an initial velocity of 2ms−1 in the x - direction at t = 0 and an electric field of 2NC−1 is switched on in the x - direction, then the range (R) of the block on the ground will be
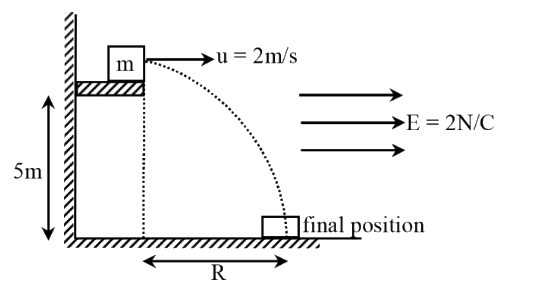
View Solution
