A vessel completely filled with water has holes 'A' and 'B' at depths 'h' and '3h' from the top respectively. Hole 'A' is a square of side 'L' and 'B' is circle of radius 'r'. The water flowing out per second from both the holes is same. Then 'L' is equal to
r12(π)12(3)12
r(π)14(3)14
r(π)12(3)14
r12(π)13(3)12
The correct Answer is:C
To solve the problem, we need to find the relationship between the side length L of the square hole A and the radius r of the circular hole B given that the water flowing out per second from both holes is the same.
1. Identify the Areas of the Holes:
- The area of hole A (square) is given by:
AA=L2
- The area of hole B (circle) is given by:
AB=πr2
2. Determine the Velocities of Efflux:
- The velocity of efflux from hole A at depth h is:
VA=√2gh
- The velocity of efflux from hole B at depth 3h is:
VB=√2g⋅3h=√6gh
3. Use the Discharge Equation:
- The discharge Q from each hole can be expressed as:
QA=AA⋅VA=L2⋅√2gh
QB=AB⋅VB=πr2⋅√6gh
- Since the discharges are equal, we set QA=QB:
L2⋅√2gh=πr2⋅√6gh
4. Cancel Common Terms:
- We can cancel √gh from both sides:
L2⋅√2=πr2⋅√6
5. Rearranging the Equation:
- Rearranging gives:
L2=πr2⋅√6√2=πr2⋅√3
6. Taking the Square Root:
- Taking the square root of both sides:
L=r⋅√π⋅√3
Final Expression:
Thus, we find that:
L=r⋅√π√3
- The area of hole A (square) is given by:
AA=L2
- The area of hole B (circle) is given by:
AB=πr2
- The velocity of efflux from hole A at depth h is:
VA=√2gh
- The velocity of efflux from hole B at depth 3h is:
VB=√2g⋅3h=√6gh
- The discharge Q from each hole can be expressed as:
QA=AA⋅VA=L2⋅√2gh
QB=AB⋅VB=πr2⋅√6gh
- Since the discharges are equal, we set QA=QB:
L2⋅√2gh=πr2⋅√6gh
- We can cancel √gh from both sides:
L2⋅√2=πr2⋅√6
- Rearranging gives:
L2=πr2⋅√6√2=πr2⋅√3
- Taking the square root of both sides:
L=r⋅√π⋅√3
Thus, we find that:
L=r⋅√π√3
Similar Questions
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA tank is filled with water and two holes A and B are made in it.- For getting same range, ratio of h' and h is

View Solution
Knowledge Check
A large open tank has two holes in the wall. One is square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth of 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then R is equal to
AL/√(2π)B2πLCLDL/2πA tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
Athe volume of water flowing out per second will decreaseBthe velocity of outflow of water remains unchangedCthe volume of water volume out per second remains zeroDBoth (b) and (c)
A closed vessel is half filled with water. There is a hole near the top of vessel and air is pumped out from this hole.
View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density ρ and height h is filled over another liquid of density 2ρ. Speeds of liquid ejecting from two holes are say v1 and v2.

The ratio v1v2 will be
View SolutionWater pours out rate of Q from a tap, into a cylindrical vessel of radius r. The rate at which the height of water level rises the height is h, is
View SolutionThe area of two holes A and B are 2a and a, respectively, The holes are at height (H/3)and(2H/3) from the surface of water. Find the correct option(s):
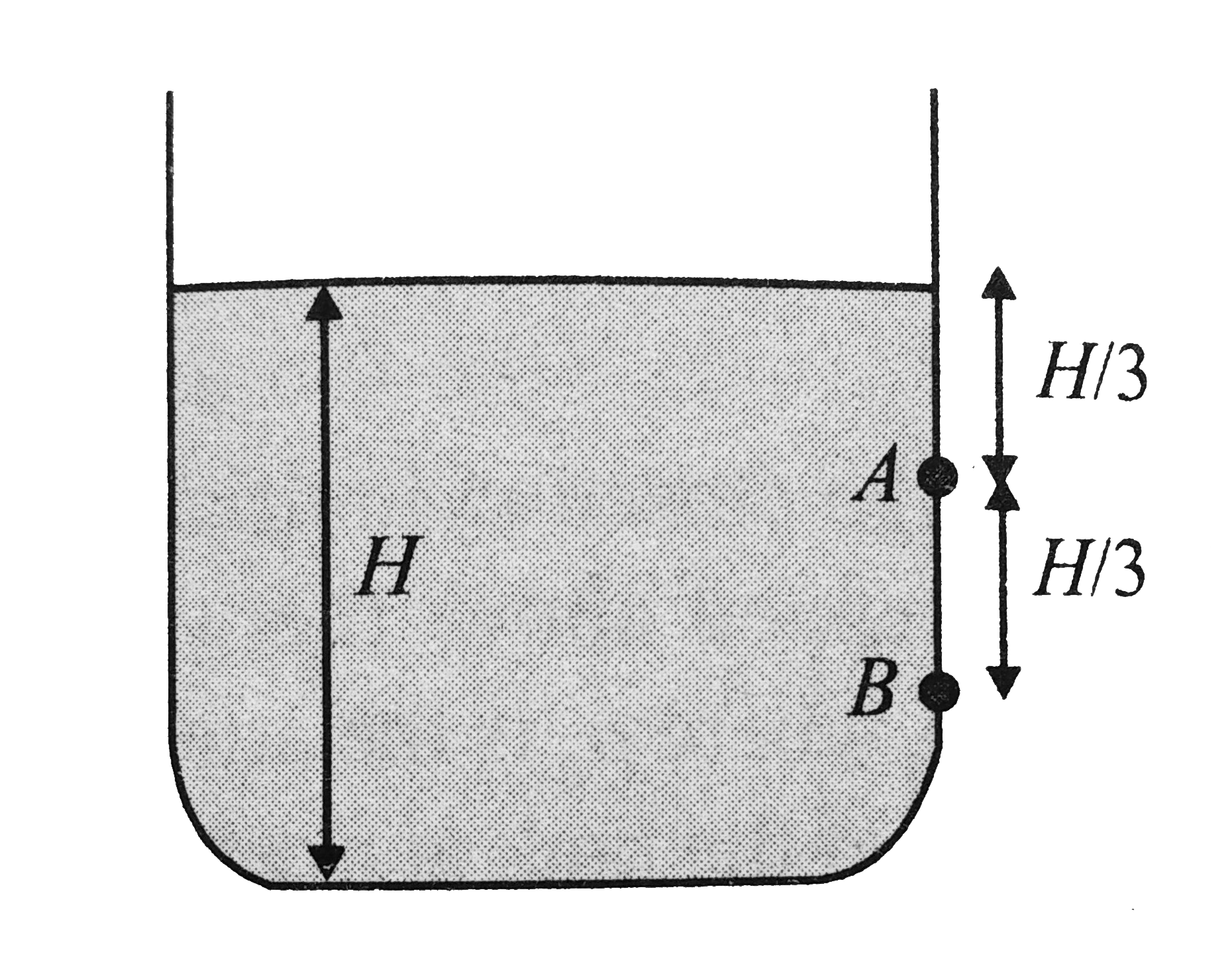
View SolutionA cylindrical vessel of 92 cm height is kept filled upto to brim. It has four holes 1,2,3 and 4 which are respectively at heights of 20cm, 30cm, 46cm and 80cm from the horizontal floor. The water falling at the maximum horizontal distance from the vessel comes from :
View SolutionIn a cylindrical water tank there are two small holes Q and P on the wall at a depth of h1 from the upper level of water and at a height of h2 from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of h1 and h2 is

View Solution
