A cylindrical vessel of 92 cm height is kept filled upto to brim. It has four holes 1,2,3 and 4 which are respectively at heights of 20cm, 30cm, 46cm and 80cm from the horizontal floor. The water falling at the maximum horizontal distance from the vessel comes from :
hole 4
hole 3
hole 2
hole 1
The correct Answer is:B
To solve the problem, we need to determine from which hole the water will fall at the maximum horizontal distance when it exits the cylindrical vessel. The key to this problem lies in understanding the relationship between the height of the holes and the range of the water jet.
1. Identify the Heights of the Holes:
- The heights of the holes from the floor are:
- Hole 1: 20 cm
- Hole 2: 30 cm
- Hole 3: 46 cm
- Hole 4: 80 cm
2. Understand the Efflux Velocity:
- The efflux velocity of water coming out of a hole at a height h from the surface of the water is given by the formula:
v=√2g(92−h)
- Here, g is the acceleration due to gravity, and 92 cm is the total height of the vessel.
3. Determine the Time of Flight:
- The time of flight t for the water to fall from height h to the ground can be calculated using the kinematic equation:
h=12gt2
- Rearranging gives:
t=√2hg
4. Calculate the Horizontal Range:
- The horizontal range R can be calculated using the formula:
R=v⋅t
- Substituting the expressions for v and t:
R=√2g(92−h)⋅√2hg=2√h(92−h)
5. Maximize the Range:
- To find the height h that maximizes the range R, we need to maximize the expression R2=4h(92−h).
- This is a quadratic function in terms of h, which opens downwards (since the coefficient of h2 is negative).
6. Find the Maximum Value:
- The maximum value occurs at:
h=922=46 cm
- This corresponds to Hole 3.
7. Conclusion:
- The water falling at the maximum horizontal distance from the vessel comes from Hole 3, which is at a height of 46 cm.
Final Answer:
The water falling at the maximum horizontal distance comes from Hole 3 (46 cm).
- The heights of the holes from the floor are:
- Hole 1: 20 cm
- Hole 2: 30 cm
- Hole 3: 46 cm
- Hole 4: 80 cm
- The efflux velocity of water coming out of a hole at a height h from the surface of the water is given by the formula:
v=√2g(92−h)
- Here, g is the acceleration due to gravity, and 92 cm is the total height of the vessel.
- The time of flight t for the water to fall from height h to the ground can be calculated using the kinematic equation:
h=12gt2
- Rearranging gives:
t=√2hg
- The horizontal range R can be calculated using the formula:
R=v⋅t
- Substituting the expressions for v and t:
R=√2g(92−h)⋅√2hg=2√h(92−h)
- To find the height h that maximizes the range R, we need to maximize the expression R2=4h(92−h).
- This is a quadratic function in terms of h, which opens downwards (since the coefficient of h2 is negative).
- The maximum value occurs at:
h=922=46 cm
- This corresponds to Hole 3.
- The water falling at the maximum horizontal distance from the vessel comes from Hole 3, which is at a height of 46 cm.
The water falling at the maximum horizontal distance comes from Hole 3 (46 cm).
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Hydrostatics)
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Surface Tension)
26 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)
20 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
A cylindrical vessel of 90cm height is kept filled up to the brim. It has four holes 1,2,3 and 4 which are, respectively, at heights of 20cm,30cm,40cm and 50cm from the horizontal floor PQ. The water falling at the maximum horizontal distance from the vessel comes from

View SolutionA cylindrical vessel of 90cm height is kept filled up to the brim. It has four holes 1,2,3 and 4 which are, respectively, at heights of 20cm,30cm,40cm and 50cm from the horizontal floor PQ. The water falling at the maximum horizontal distance from the vessel comes from

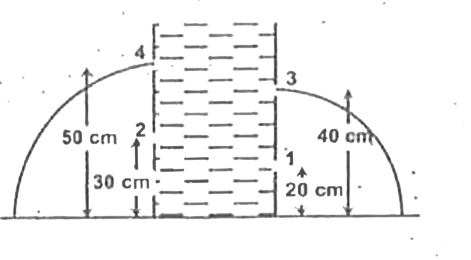
View SolutionFigure shows a cylindrical vessel of height 90 cm filled upto the brim . There are four holes in the vessel as shows in figure . The liquid falling at maximum horizontal distance from the vessel would come from
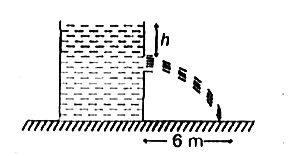
View SolutionA liquid is coming out from the orifice of tank and falls upto a maximum horizontal distance of 6 m. The height h is equal to
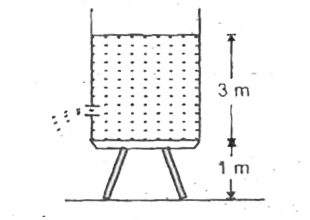
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
View SolutionWater level is maintained ina cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.

View SolutionA tank of height H is fully filled with water. If the water rushing from a hole made in the tank below the free surface , strikes the floor at a maximum horizontal distance , then the depth of the hole from the free surface must be
View SolutionA cylindrical vessel of height 24 cm and diamater 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.
View SolutionA vessel in the form of inverted cone. Its height is 8 cm and radius of its top, which is open, is 5 cm. It is filled with water upto the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped in the vessel, one fourth of the water flows out. Find the number of lead shots dropped in the vessel.
View SolutionA wide cylindrical vessel 50cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
View Solution
