The length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. The natural length of the wire is
l1+l22
√l1l2
l1T2−l2T1T2−T1
l1T2+l2T1T2+T1
To find the natural length of the metal wire when given its lengths under different tensions, we can follow these steps:
1. Understand the Problem: We have a metal wire that stretches under tension. The lengths of the wire under two different tensions are given as l1 and l2 for tensions T1 and T2 respectively. We need to find the natural length L of the wire (the length of the wire without any tension).
2. Define the Relationship: The elongation (change in length) of the wire can be expressed using Young's modulus E:
Stress=TAandStrain=ΔLL
From Young's modulus, we know:
E=StressStrain=T/AΔL/L
Rearranging gives us:
ΔL=T⋅LA⋅E
3. Calculate Elongation for Each Case:
- For the first tension T1:
ΔL1=l1−L=T1⋅LA⋅E
- For the second tension T2:
ΔL2=l2−L=T2⋅LA⋅E
4. Set Up Equations:
- Rearranging the equations gives:
l1−L=T1⋅LA⋅E(1)
l2−L=T2⋅LA⋅E(2)
5. Express L in Terms of l1 and l2:
- From (1):
L=l1−T1⋅LA⋅E
- From (2):
L=l2−T2⋅LA⋅E
6. Equate and Solve:
- Setting the two expressions for L equal gives:
l1−T1⋅LA⋅E=l2−T2⋅LA⋅E
- Rearranging leads to:
l1−l2=L(T1−T2A⋅E)
- Solving for L:
L=l1T2−l2T1T2−T1
Final Expression:
Thus, the natural length L of the wire is given by:
L=l1T2−l2T1T2−T1
Stress=TAandStrain=ΔLL
From Young's modulus, we know:
E=StressStrain=T/AΔL/L
Rearranging gives us:
ΔL=T⋅LA⋅E
- For the first tension T1:
ΔL1=l1−L=T1⋅LA⋅E
- For the second tension T2:
ΔL2=l2−L=T2⋅LA⋅E
- Rearranging the equations gives:
l1−L=T1⋅LA⋅E(1)
l2−L=T2⋅LA⋅E(2)
- From (1):
L=l1−T1⋅LA⋅E
- From (2):
L=l2−T2⋅LA⋅E
- Setting the two expressions for L equal gives:
l1−T1⋅LA⋅E=l2−T2⋅LA⋅E
- Rearranging leads to:
l1−l2=L(T1−T2A⋅E)
- Solving for L:
L=l1T2−l2T1T2−T1
Thus, the natural length L of the wire is given by:
L=l1T2−l2T1T2−T1
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Question For short Anser
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SOUND WAVESBOOK - HC VERMA ENGLISHCHAPTER - SOUND WAVESEXERCISE - All Questions
133 Videos
Similar Questions
Knowledge Check
The length of a rubber cord is l1 m when the tension is 4 N and l2 m when the tension is 6 N.The length when the tension is 9 N, is
A(2.5l2−1.5l1)mB(6l2−1.5l1)mC(3l1−l2)mD(3.5l2=−2.5l1)m
The length of a metal wire is l1 when the tension in it is F1 and l2 when the tension becomes F2. Find the natural length of wire.
View SolutionThe length of a steel wire is l1 when the stretching force is T1 and l2 when the stretching force is T2. The natural length of the wire is
View SolutionWhen the tension in a metal wire is T1, its length is I1. When the tension is T2, its length is I2. The natural length of wire is
View SolutionThe length of an elastic string is Xm when the tension is 8 N, and Y m when the tension is 10 N. The length in metres when the tension is 18 N is
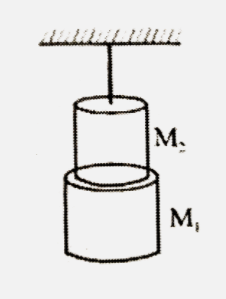
View SolutionThe length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
View Solutionan elastic spring has a length l1 when tension in it is 4N. Its length is l2 when tension in it is 5N. What will be its length when tension in it is 9N?
View SolutionA transverse wave travels on a taut steel wire with a velocity of when tension in it is 2.06×104N . When the tension is changed to T, the velocity changed to 3v. The value of T is close to :
View Solution
