A non -uniform rod of length l having mass density λ(x)=(A+Bx2) is placed - x - axis with its ends at , (a,0)and(a+l,0) . The force it would exert on a point mass m kept at the origin is
Gm[A(la(a+2))+Bl]
Gm[A(la(a−l))−Bl]
Gm[A(la(a+l))+Bl]
Gm[A(la(a+l))−Bl]
The correct Answer is:C
To solve the problem of finding the gravitational force exerted by a non-uniform rod on a point mass m located at the origin, we can follow these steps:
Step 1: Define the mass density and the rod's position
The mass density of the rod is given by:
λ(x)=A+Bx2
The rod is placed along the x-axis from x=a to x=a+l.
Step 2: Express the mass element
To find the gravitational force, we need to consider a small mass element dm of the rod. The mass element can be expressed as:
dm=λ(x)dx=(A+Bx2)dx
where dx is an infinitesimal length of the rod.
Step 3: Determine the force due to the mass element
The gravitational force dF exerted by the mass element dm at a distance x from the point mass m located at the origin is given by Newton's law of gravitation:
dF=Gmdmx2
Substituting dm from the previous step:
dF=Gm(A+Bx2)dxx2
Step 4: Simplify the expression for dF
We can simplify dF:
dF=Gm(Ax2+B)dx
Step 5: Set up the integral for total force
To find the total force F exerted by the entire rod on the mass m, we need to integrate dF from x=a to x=a+l:
F=∫a+ladF=∫a+laGm(Ax2+B)dx
Step 6: Evaluate the integral
This integral can be split into two parts:
F=Gm(∫a+laAx2dx+∫a+laBdx)
1. First integral:
∫Ax2dx=−Ax
Evaluating from a to a+l:
−Aa+l+Aa=A(1a−1a+l)=A((a+l)−aa(a+l))=Ala(a+l)
2. Second integral:
∫Bdx=Bx
Evaluating from a to a+l:
B(a+l)−Ba=Bl
Step 7: Combine the results
Now, substituting back into the expression for F:
F=Gm(Ala(a+l)+Bl)
Final Result
Thus, the total gravitational force exerted by the rod on the mass m at the origin is:
F=Gm(Ala(a+l)+Bl)
The mass density of the rod is given by:
λ(x)=A+Bx2
The rod is placed along the x-axis from x=a to x=a+l.
To find the gravitational force, we need to consider a small mass element dm of the rod. The mass element can be expressed as:
dm=λ(x)dx=(A+Bx2)dx
where dx is an infinitesimal length of the rod.
The gravitational force dF exerted by the mass element dm at a distance x from the point mass m located at the origin is given by Newton's law of gravitation:
dF=Gmdmx2
Substituting dm from the previous step:
dF=Gm(A+Bx2)dxx2
We can simplify dF:
dF=Gm(Ax2+B)dx
To find the total force F exerted by the entire rod on the mass m, we need to integrate dF from x=a to x=a+l:
F=∫a+ladF=∫a+laGm(Ax2+B)dx
This integral can be split into two parts:
F=Gm(∫a+laAx2dx+∫a+laBdx)
∫Ax2dx=−Ax
Evaluating from a to a+l:
−Aa+l+Aa=A(1a−1a+l)=A((a+l)−aa(a+l))=Ala(a+l)
∫Bdx=Bx
Evaluating from a to a+l:
B(a+l)−Ba=Bl
Now, substituting back into the expression for F:
F=Gm(Ala(a+l)+Bl)
Thus, the total gravitational force exerted by the rod on the mass m at the origin is:
F=Gm(Ala(a+l)+Bl)
Similar Questions
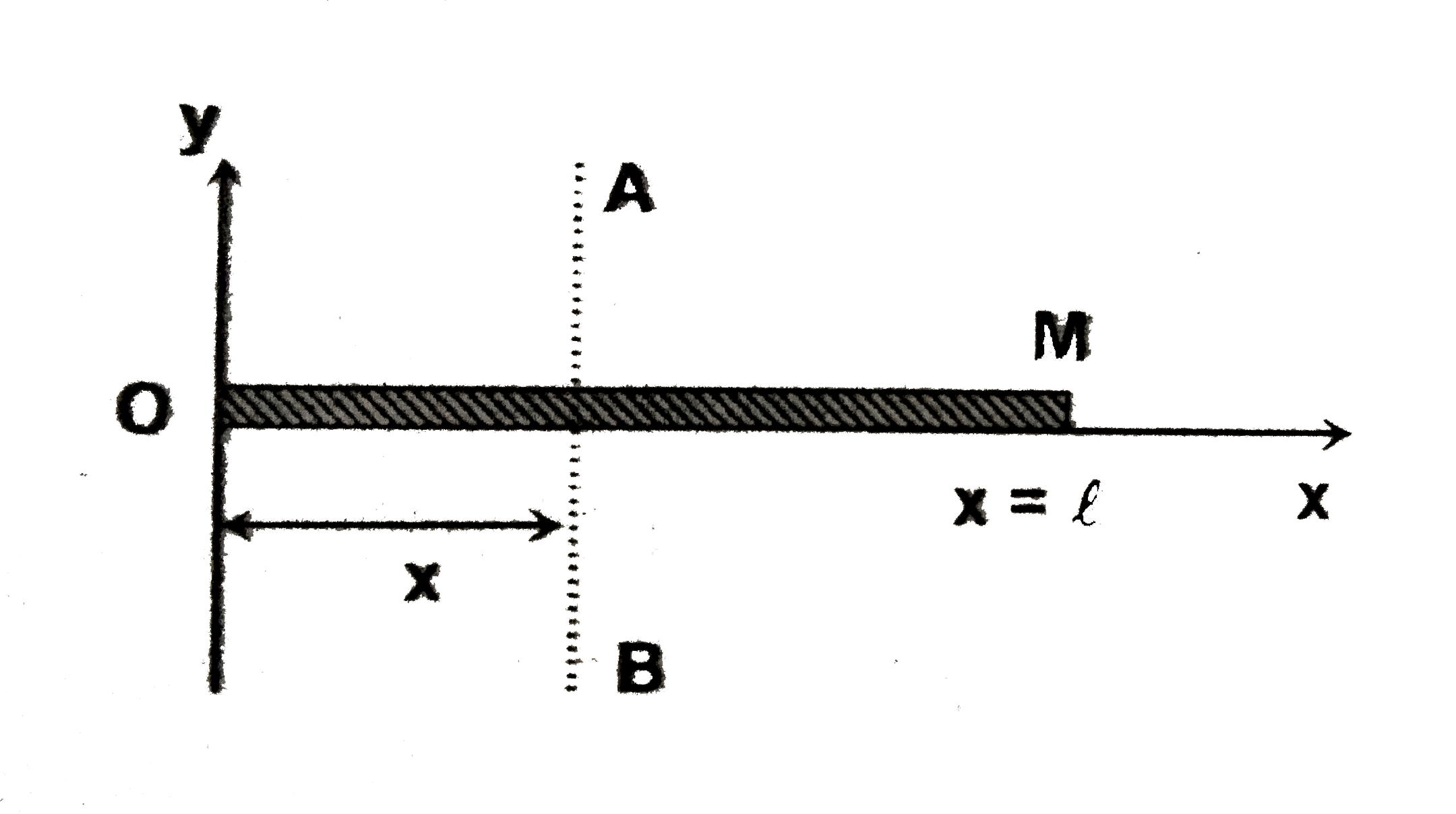
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass density that varies with the distance x from left end of the rod according to λ=λ0(x3L3)
Where unit of λ0 is kg/m. What is the value of x so that moment of inertia of rod about axis AB (IAB) is minimum?
View Solution
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass densty that varies with the distance x from left end of the rod according to λ=λ0(x3L3)
Where unit of λ0 is kg/m. What is the value of x so that moment of inertia of rod about axis AB (IAB) is minimum?
View Solution
Knowledge Check
The density of a non-uniform rod of length 1m is given by ρ(x)=a(1+bx2)
where a and b are constants and 0≤x≤1.
The centre of mass of the rod will be atA3(2+b)4(3+b)B4(2+b)3(3+b)C3(3+b)4(2+b)D4(3+b)3(2+b)
The moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is

View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View SolutionThe linear density of a non−uniform rod of length 2m is given by λ(x)=a(1+bx2) where a and b are constants and 0≤x≤2. The centre of mass of the rod will be at. X=
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionMass is non-uniformly distributed over the rod of length l, its linear mass density varies linearly with length as λ=kx2. The position of centre of mass (from lighter end) is given by-
View SolutionA uniform thin rod AB of length L has linear mass density μ(x)=a+bxL, where x is measured from A. If the CM of the rod lies at a distance of (712L) from A, then a and b are related as :_
View SolutionThe density of a non-uniform rod of length 1m is given by ρ(x)=a(1+bx2)
where a and b are constants and 0≤x≤1.
The centre of mass of the rod will be at
View Solution
