Question

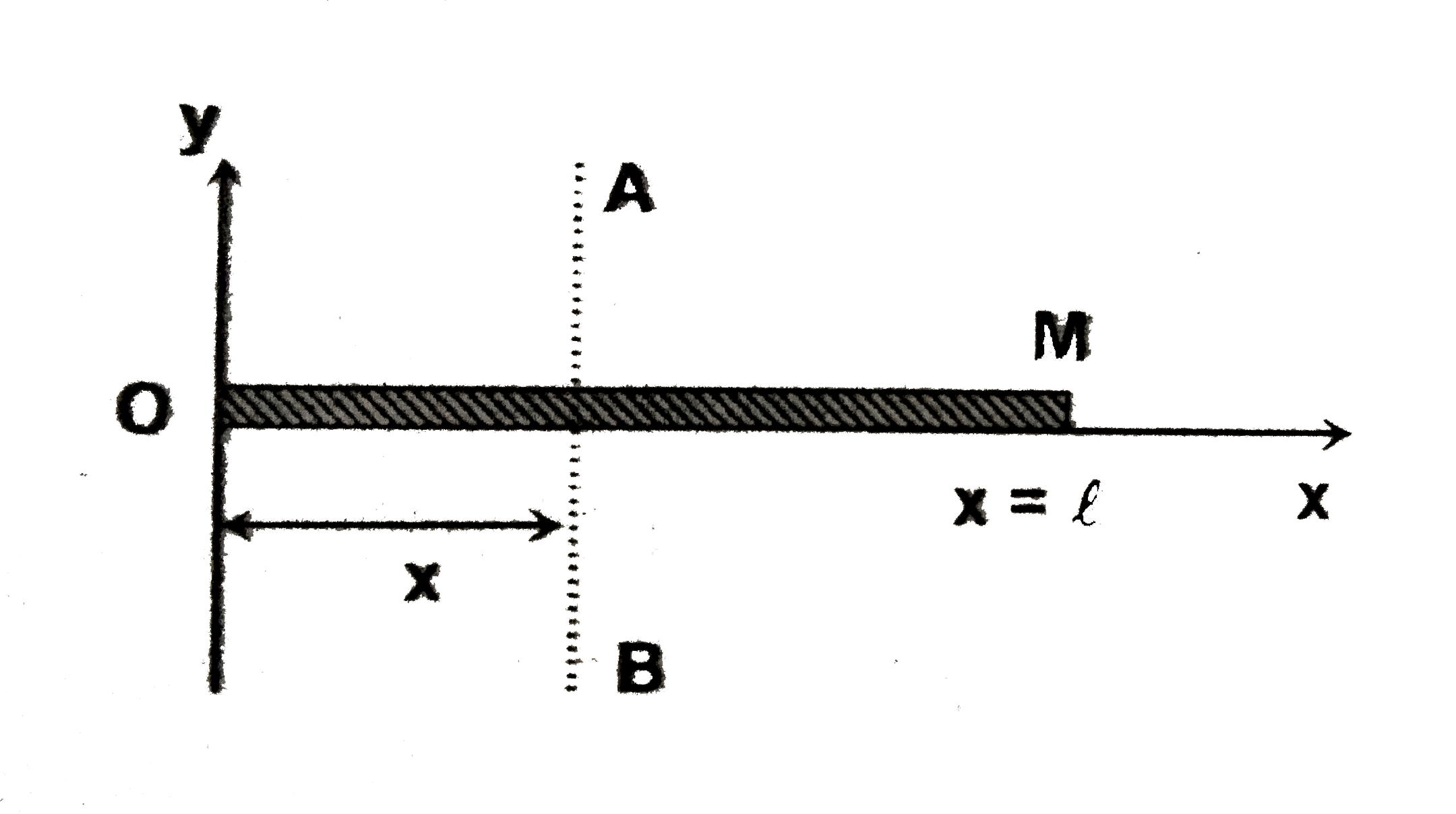
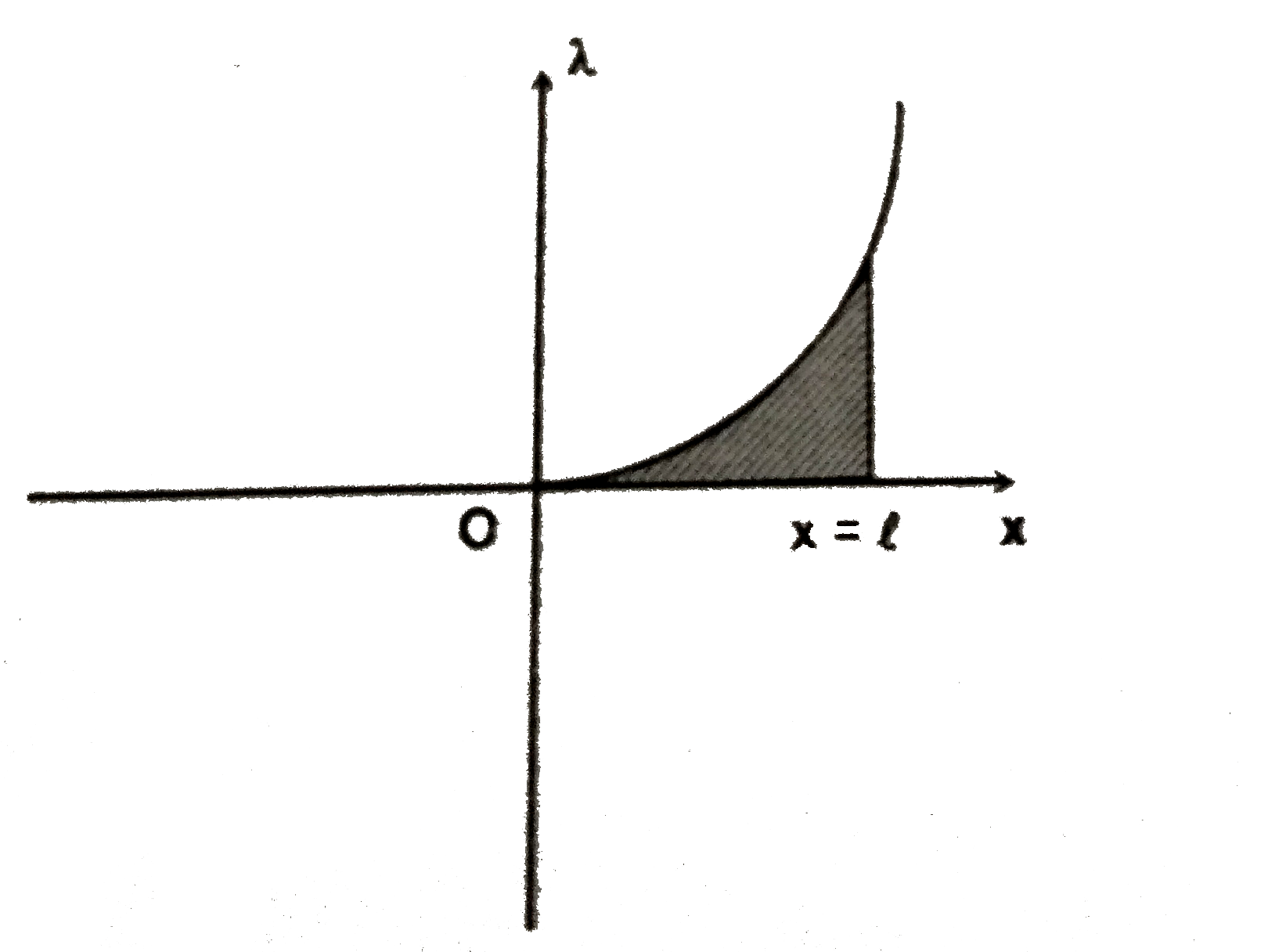
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass densty that varies with the distance x from left end of the rod according to $\lambda ={\lambda }_0\left(\frac{x^3}{L^3}\right)$
Where unit of ${\lambda }_0$ is kg/m. What is the value of x so that moment of inertia of rod about axis AB $\left(I_{AB}\right)$ is minimum?

Options

A. `(7l)/(15)`
B. `(2l)/(5)`
C. `(8l)/(15)`
D. `(4l)/(5)`

Answer

D

Explanation

First method:
`I_(AB)=inty^(2)dm=(lamda_(0))/(l^(3))int_(-x)^(l-x)(y+x)^(3)y^(2)dy`
`int(y+x)^(3)y^(2)dy=y^(2)((y+x)^(4))/(4)-(1)/(2)y(y+x)^(4)dy`
`=(y^(2)(y+x)^(2))/(4)-(y)/(10)(y+x)^(5)+(1)/(10)(y+x)^(5)dy`
`=(y^(2)(y+x)^(2))/(4)-(y(x+y)^(5))/(10)+((y+x)^(2))/(60)`
`int_(-x_(0))^((l-x))y^(2)(y+x)^(3)dx=((L-x)^(2)(l)^(4))/(4)-((l-x)l^(5))/(10)+(l^(6))/(60)`
`I_(AB)=lamda_(0)[((l-x)^(2))/(4)l-(1)/(10)(l-x)l^(2)+(1)/(60)l^(3)]=lamda_(0)l[((l-x)^(2))/(4)l-(1)/(10)(l-x)+(1)/(60)l^(2)]`
`(dl_(AB))/(dx)=0implies-((l-x))/(2)+(l)/(10)=0implies5l-5x=l" "implies 5x=4l" "implies" "x=(4l)/(5)`
Second method:
As we know that moment of inertial is minimum among all set of parallel axis, if axis is passing through centre of mass, so x must be distance of centre of mass.
`X_(CM)=(1)/(M)int_(0)^(L)xdm`
`M=intdm=(lamda_(0))/(l^(3))underset(0)overset(l)intx^(3)dx=(lamda_(0)l)/(4)` and `underset(0)overset(l)intxdx=(lamda_(0))/(l^(3))underset(0)overset(l)intx^(4)dx=(lamda_(0)l^(2))/(5)`
Putting these values in equation (i) we have `x_(CM)=(4l)/(5)`
Third method:
From given funtion it is clear that centre of mass of system must be at distance grater
that l/2. We have only two option `(8l)/(15)` and `(4l)/(5)`. For graph it is clear that maximum mass existence is nearer to other end, so it can't be `(8l)/(15)`, so right answer will be `(4l)/(5)`