Consider two objects of different masses connected by a cable passing over a massless and frictionless Pulley. Derive expressions for the tension in the cable and acceleration of the objects.
To derive the expressions for the tension in the cable and the acceleration of the objects connected by a massless and frictionless pulley, we will consider two masses, m1 and m2, connected by a cable over the pulley. We will analyze two cases: when m1>m2 and when m2>m1.
Case 1: m1>m2
1. Identify Forces:
- The weight of mass m1 acting downwards: Fg1=m1g
- The weight of mass m2 acting downwards: Fg2=m2g
- Tension in the cable: T
2. Write the equations of motion:
- For mass m1 (moving down):
m1g−T=m1a(1)
- For mass m2 (moving up):
T−m2g=m2a(2)
3. Add the equations:
(m1g−T)+(T−m2g)=m1a+m2a
Simplifying gives:
m1g−m2g=(m1+m2)a
(m1−m2)g=(m1+m2)a
4. Solve for acceleration a:
a=(m1−m2)gm1+m2
5. Substitute a back to find tension T:
Using equation (1):
m1g−T=m1a
Substituting for a:
T=m1g−m1((m1−m2)gm1+m2)
Simplifying gives:
T=2m1m2gm1+m2
Case 2: m2>m1
1. Identify Forces:
- The weight of mass m2 acting downwards: Fg2=m2g
- The weight of mass m1 acting downwards: Fg1=m1g
- Tension in the cable: T
2. Write the equations of motion:
- For mass m2 (moving down):
m2g−T=m2a(1)
- For mass m1 (moving up):
T−m1g=m1a(2)
3. Add the equations:
(m2g−T)+(T−m1g)=m2a+m1a
Simplifying gives:
m2g−m1g=(m1+m2)a
(m2−m1)g=(m1+m2)a
4. Solve for acceleration a:
a=(m2−m1)gm1+m2
5. Substitute a back to find tension T:
Using equation (1):
m2g−T=m2a
Substituting for a:
T=m2g−m2((m2−m1)gm1+m2)
Simplifying gives:
T=2m1m2gm1+m2
Final Expressions
- Acceleration:
a=|m1−m2|gm1+m2
- Tension:
T=2m1m2gm1+m2
- The weight of mass m1 acting downwards: Fg1=m1g
- The weight of mass m2 acting downwards: Fg2=m2g
- Tension in the cable: T
- For mass m1 (moving down):
m1g−T=m1a(1)
- For mass m2 (moving up):
T−m2g=m2a(2)
(m1g−T)+(T−m2g)=m1a+m2a
Simplifying gives:
m1g−m2g=(m1+m2)a
(m1−m2)g=(m1+m2)a
a=(m1−m2)gm1+m2
Using equation (1):
m1g−T=m1a
Substituting for a:
T=m1g−m1((m1−m2)gm1+m2)
Simplifying gives:
T=2m1m2gm1+m2
- The weight of mass m2 acting downwards: Fg2=m2g
- The weight of mass m1 acting downwards: Fg1=m1g
- Tension in the cable: T
- For mass m2 (moving down):
m2g−T=m2a(1)
- For mass m1 (moving up):
T−m1g=m1a(2)
(m2g−T)+(T−m1g)=m2a+m1a
Simplifying gives:
m2g−m1g=(m1+m2)a
(m2−m1)g=(m1+m2)a
a=(m2−m1)gm1+m2
Using equation (1):
m2g−T=m2a
Substituting for a:
T=m2g−m2((m2−m1)gm1+m2)
Simplifying gives:
T=2m1m2gm1+m2
- Acceleration:
a=|m1−m2|gm1+m2
- Tension:
T=2m1m2gm1+m2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - SHORT ANSWER TYPE QUESTION
7 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
13 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
Two blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure. The acceleration of the blocks is :
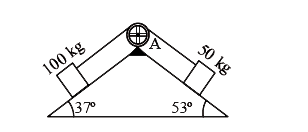
View SolutionExplain the motion of an object suspended by a cable that passes over a pulley and horizontally connected at the other end to a second object that rests on a smooth horizontal table. Derive expressions for tension in the cable and acceleration of the objects.
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
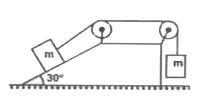
View SolutionTwo blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
View SolutionFig. shows a block of mass m1 resting on a smooth surface. It is connected to a mass m2 by a string passing over a massless and frictionaless pulleys m2>m1. The acceleration of the hanging mass m2 is :

View SolutionA block of mass M1=3kg on a smooth fixed inclined plane of angle 30∘ is connected by a cord over a small frictionless pulley to a second block mass 2kg hanging vertically. The tension in the cord and the acceleration of each block are ………............. and ...................... respectively.

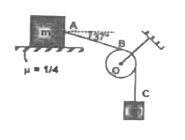
View SolutionTwo blocks of same mass 'm' are connected by the cable passing over a pulley of mass 'm' and radius 'R'. There is no slipping between the pulley and the cable. The coefficient of friction between the block 'A' and the horizontal surface is 1/4 . At the moment shown in the figure,the tension in the cable AB is
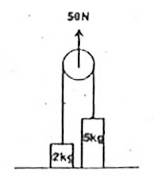
View SolutionTwo blocks of masses 2kg and 5kg are at rest on ground. The masses are connected by a string passing over a frictionless pulley which is under the influence of a constant upward force F = 50 N. Find the accelerations of 5kg and 2kg masses.
View SolutionTwo blocks of mass 2 kg and 5 kg are at rest on the ground. The masses are connected by a string passing over a frictionless pulley which is under the influence of a constant upward force F = 50N. The acceleration of 5 kg and 2 kg masses are
View Solution
