If V and u are electric potential and energy density, respectively, at a distance r from a positive point charge, then which of the following graph is correct ?
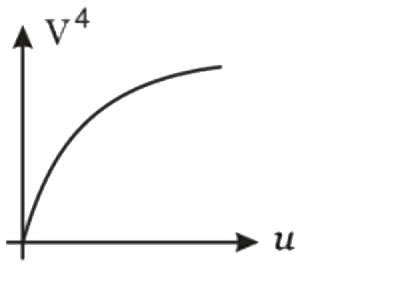
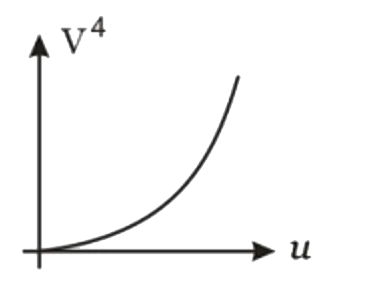
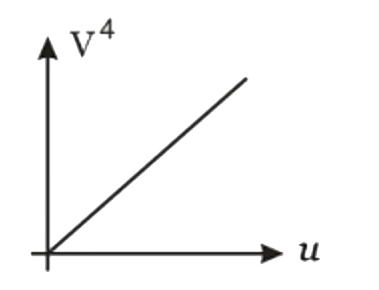
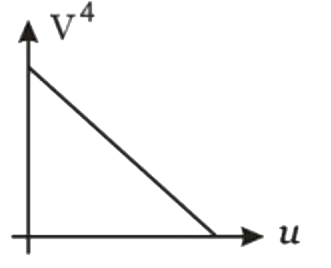
The correct Answer is:C
To solve the problem, we need to establish the relationship between electric potential (V) and energy density (U) at a distance r from a positive point charge. Here’s a step-by-step solution:
Step 1: Understand the Electric Potential (V)
The electric potential (V) at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant.
Step 2: Understand the Electric Field (E)
The electric field (E) at a distance r from a point charge Q is given by:
E=kQr2
Step 3: Calculate the Energy Density (U)
The energy density (U) in an electric field is given by the formula:
U=12ϵ0E2
where ϵ0 is the permittivity of free space.
Step 4: Substitute E into the Energy Density Formula
Now, substituting the expression for E into the energy density formula:
U=12ϵ0(kQr2)2
U=12ϵ0k2Q2r4
Step 5: Relate U to V
From the expression for V, we can express r in terms of V:
r=kQV
Now substituting this into the expression for U:
U=12ϵ0k2Q2(kQV)4
U=12ϵ0k2Q2V4k4Q4
U=ϵ0V42k2Q2
Step 6: Establish the Relationship
From the above expression, we can see that:
U∝V4
This means that energy density (U) is proportional to the fourth power of electric potential (V).
Step 7: Graphical Representation
If we plot U on the x-axis and V on the y-axis, the relationship U∝V4 suggests that the graph will be a parabolic curve opening upwards.
Step 8: Determine the Correct Graph
Since U is plotted on the x-axis and V on the y-axis, the relationship can be expressed as:
U=kV4
This indicates that the graph will be a curve that passes through the origin and rises steeply as V increases.
Conclusion
The correct graph representing the relationship between electric potential (V) and energy density (U) is a parabolic curve.
---
The electric potential (V) at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant.
The electric field (E) at a distance r from a point charge Q is given by:
E=kQr2
The energy density (U) in an electric field is given by the formula:
U=12ϵ0E2
where ϵ0 is the permittivity of free space.
Now, substituting the expression for E into the energy density formula:
U=12ϵ0(kQr2)2
U=12ϵ0k2Q2r4
From the expression for V, we can express r in terms of V:
r=kQV
Now substituting this into the expression for U:
U=12ϵ0k2Q2(kQV)4
U=12ϵ0k2Q2V4k4Q4
U=ϵ0V42k2Q2
From the above expression, we can see that:
U∝V4
This means that energy density (U) is proportional to the fourth power of electric potential (V).
If we plot U on the x-axis and V on the y-axis, the relationship U∝V4 suggests that the graph will be a parabolic curve opening upwards.
Since U is plotted on the x-axis and V on the y-axis, the relationship can be expressed as:
U=kV4
This indicates that the graph will be a curve that passes through the origin and rises steeply as V increases.
The correct graph representing the relationship between electric potential (V) and energy density (U) is a parabolic curve.
Similar Questions
E, U and K represent total mechanical energy. potential energy and kinetic energy respectively of a satellite revolving around a planet, then which of the following is correct?
View SolutionElectric potential V due to a short dipole is related to the distance r of the observation point as
View SolutionShow that electric potential at a point P, at a distance .r. from a fixed point charge Q, is given by :
V=(14πε0)Qr
View SolutionIn a uniform electric field, a point charge of mass m and charge q is released from rest. If there are no other forces acting on the particle, then which of the following graphs, correctly show the dependence of the particles speed v on the distance x travelled by the particles speed v on the distance x travelled by it? [Graphs are schmatic and not drawn to scale]
View SolutionThe electric potential at a certain distance from a point charge is 600 V and the electric field is 200NC−1. Which of the following statements will be true?
View SolutionObtain an expression for electric potential .V due to a point charge .Q at a distance r.
View SolutionIn the figure shown the potential energy U of a particle is plotted its position 'x' from origin. Then which of the following statement is correct A particle at :

View SolutionThe distance v of the real image formed by a convex lens is measured for various object distance u. A graph is poltted between v and u, which one of the following graphs is correct
View SolutionThree concentric charged metallic spherical shells A, B and C have radii a,b and c, charge densities σ,−σ and σ and potentials VA,VB and VC respectively. Then which of the following relations is correct?
View SolutionThe gravitational potential energy at a body of mass m at a distance r from the centre of the earth is U. What is the weight of the body at this distance ?
View Solution
