E, U and K represent total mechanical energy. potential energy and kinetic energy respectively of a satellite revolving around a planet, then which of the following is correct?

A

K = E

B

U= 2E

C

$K = | E |$

D

Both (2) and (3)

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:D

To solve the problem, we need to analyze the relationships between the total mechanical energy (E), potential energy (U), and kinetic energy (K) of a satellite revolving around a planet.
1. Define the Energies:
- The kinetic energy (K) of the satellite is given by the formula:
$K = \frac{1}{2} m v^{2}$
- The potential energy (U) of the satellite due to gravitational attraction is given by:
$U = - \frac{G M m}{r}$
where $G$ is the gravitational constant, $M$ is the mass of the planet, $m$ is the mass of the satellite, and $r$ is the distance from the center of the planet to the satellite.
2. Centripetal Force and Gravitational Force:
- For the satellite to remain in circular motion, the gravitational force must provide the necessary centripetal force:
$\frac{G M m}{r^{2}} = \frac{m v^{2}}{r}$
- Simplifying this equation by canceling $m$ from both sides gives:
$\frac{G M}{r^{2}} = \frac{v^{2}}{r}$
- Rearranging leads to:
$v^{2} = \frac{G M}{r}$
3. Substituting Kinetic Energy:
- Substitute $v^{2}$ into the kinetic energy formula:
$K = \frac{1}{2} m (\frac{G M}{r}) = \frac{G M m}{2 r}$
4. Total Mechanical Energy:
- The total mechanical energy (E) is the sum of kinetic and potential energy:
$E = K + U$
- Substituting the expressions for K and U:
$E = \frac{G M m}{2 r} - \frac{G M m}{r} = \frac{G M m}{2 r} - \frac{2 G M m}{2 r} = - \frac{G M m}{2 r}$
5. Relationship Between Energies:
- From the calculations, we find:
- $K = \frac{G M m}{2 r}$
- $U = - \frac{G M m}{r}$
- $E = - \frac{G M m}{2 r}$
6. Analyzing the Relationships:
- The kinetic energy is positive, while the potential energy is negative.
- The total mechanical energy is negative and equal to half of the potential energy (in magnitude):
$U = 2 E and K = - E$
Conclusion:
From the analysis, we conclude:
- $U = 2 E$
- $K = - E$
- The relationships show that both kinetic and potential energies are related to the total mechanical energy.
Final Answer:
The correct relationships are:
- Option 2: $U = 2 E$ is correct.
- Option 3: $K = - E$ is also correct.
- Therefore, the best option is option 4, which states that both 2 and 3 are correct.

Updated on:18/9/2024

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

The potential energy function for a particle executing linear SHM is given by $V (x) = \frac{1}{2} k x^{2}$ where k is the force constant of the oscillator. For $k = 0.5 N m^{- 1}$ , the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches $x = \pm x_{m}$ .if V and K indicate the potential energy and kinetic energy respectively of the particle at $x = + x_{m}$ ,then which of the following is correct?

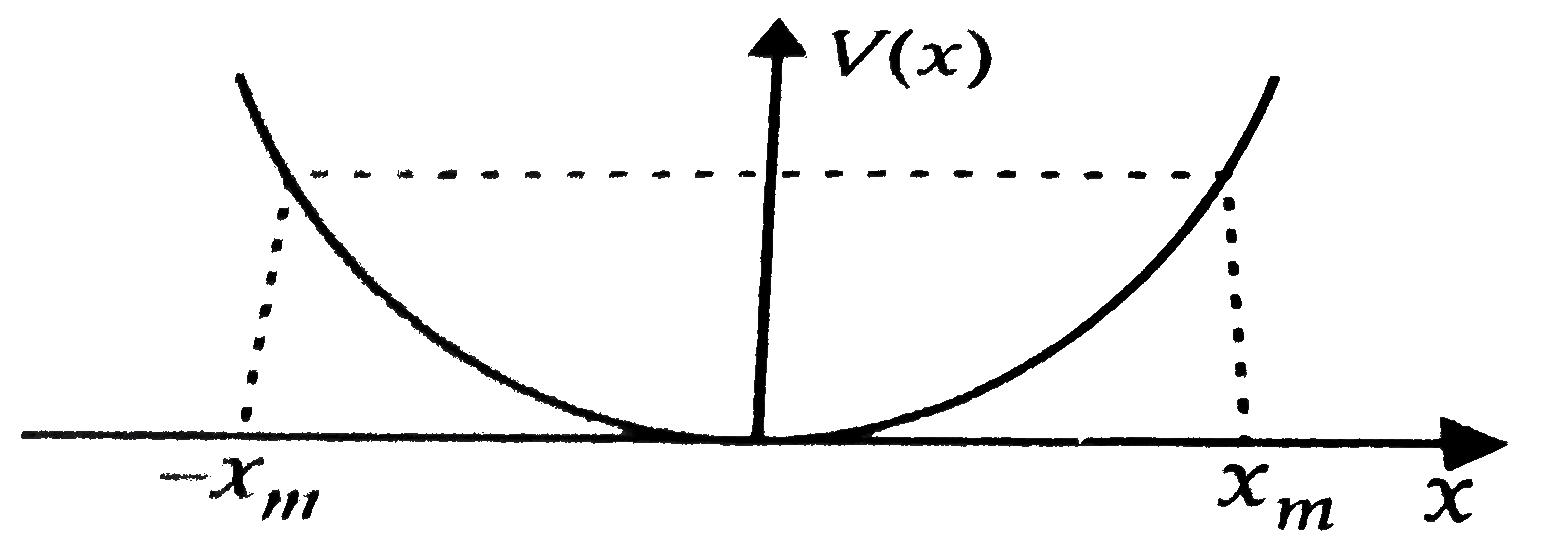AV=0, K=E
BV=E, K=0
CV lt K, K=0
DV=0, K lt E
If $E_{p} and E_{x}$ represent potential energy and kinetic energy.respectively, of an orbital electron, then, according to Bohr.s theory :
A $E_{k} = - E_{p} / 2$
B $E_{k} = - E_{p}$
C $E_{k} = - 2 E_{P}$
D $E_{k} 2 E_{P}$

AAKASH INSTITUTE ENGLISH-MOCK TEST 13-Example

Home
Ask Doubt
Profile