Determine the maximum acceleration of the truck in which a box lying on the floor of its back will remain stationary, given that the coefficient of static friction between the box and truck's floor is 0.2.
To determine the maximum acceleration of the truck such that the box remains stationary on its floor, we can follow these steps:
Step 1: Understand the Forces Acting on the Box
When the truck accelerates, the box experiences a pseudo force acting in the opposite direction of the truck's acceleration. The forces acting on the box are:
- The gravitational force (weight) acting downwards: mg
- The normal force acting upwards: N
- The static friction force acting horizontally in the direction of the truck's acceleration: f
Step 2: Write the Equation for Static Friction
The maximum static friction force that can act on the box is given by:
fmax=μN
where μ is the coefficient of static friction and N is the normal force.
Step 3: Relate Normal Force to Weight
Since the box is not moving vertically, the normal force N is equal to the weight of the box:
N=mg
Thus, the maximum static friction can be rewritten as:
fmax=μmg
Step 4: Set Up the Equation for Pseudo Force
When the truck accelerates with acceleration a, the pseudo force acting on the box is:
fpseudo=ma
In order for the box to remain stationary relative to the truck, the static friction must be equal to or greater than the pseudo force:
fmax≥fpseudo
Substituting the expressions we have:
μmg≥ma
Step 5: Cancel Mass and Rearrange the Equation
We can cancel m from both sides (assuming m≠0):
μg≥a
This implies:
a≤μg
Step 6: Substitute the Given Values
We know that the coefficient of static friction μ=0.2 and the acceleration due to gravity g≈10m/s2:
a≤0.2×10
Calculating this gives:
a≤2m/s2
Conclusion
The maximum acceleration of the truck such that the box remains stationary on the floor is:
2m/s2
When the truck accelerates, the box experiences a pseudo force acting in the opposite direction of the truck's acceleration. The forces acting on the box are:
- The gravitational force (weight) acting downwards: mg
- The normal force acting upwards: N
- The static friction force acting horizontally in the direction of the truck's acceleration: f
The maximum static friction force that can act on the box is given by:
fmax=μN
where μ is the coefficient of static friction and N is the normal force.
Since the box is not moving vertically, the normal force N is equal to the weight of the box:
N=mg
Thus, the maximum static friction can be rewritten as:
fmax=μmg
When the truck accelerates with acceleration a, the pseudo force acting on the box is:
fpseudo=ma
In order for the box to remain stationary relative to the truck, the static friction must be equal to or greater than the pseudo force:
fmax≥fpseudo
Substituting the expressions we have:
μmg≥ma
We can cancel m from both sides (assuming m≠0):
μg≥a
This implies:
a≤μg
We know that the coefficient of static friction μ=0.2 and the acceleration due to gravity g≈10m/s2:
a≤0.2×10
Calculating this gives:
a≤2m/s2
The maximum acceleration of the truck such that the box remains stationary on the floor is:
2m/s2
Similar Questions
Detrmine the maximum acceleration of the train in which a box lying on the floor will remain stationary given that the coefficient of static friction between the box and the train s floor is 0.15 given g=10m/s2 .
View SolutionMaximum acceleration of the train in which a 50 kg box lying on its floor will ramain stationary is (Given: Co-efficient of static friction between the box and the train's floor is 0.3andg=10ms−2)
View SolutionA wooden box lying at rest on an inclined surface of a wet wood is held at static equilibrium by a constant force F applied perpendicular to the incline. If the mass of the box is 1kg, the angle of inclination is 30∘ and the coefficient of static friction between the box and the inclined plane is 0.2, the minimum magnitude of F is (Use g= 10m/s2 )
View SolutionA man of mass 75kg is pushing a heavy box on a flat floor. The coefficient of kinetic and static friction between the floor and the box is 0.20, and the coefficient of static friction between the man's shoes and the floor is 0.80. If the man pushes horizontally, what is the maximum values (in kg) of the box he can move?

View SolutionIn a rotor, a hollow vertical cylindrical structure rotates about its axis and a person rests against the inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the rotor is 2m and the coefficient of static friction between the wall and the person is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
View SolutionIN a rotor, a hollow verticla cylindrical structure rotates about its axis and a person rests asgainst he inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the roter is 2m and the coefficient of static frictioin between the wall and theperson is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionThe coefficient of friction between two surface is 0.2. The maximum angle of friction is
View SolutionA block is placed at distance of 2m from the rear on the floor of a truck (g=10ms−2). When the truck moves with an acceleration of 8ms−2, the block takes 2 sec to fall off from the rear of the truck. The coefficient of sliding friction between truck and the block is
View SolutionA uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
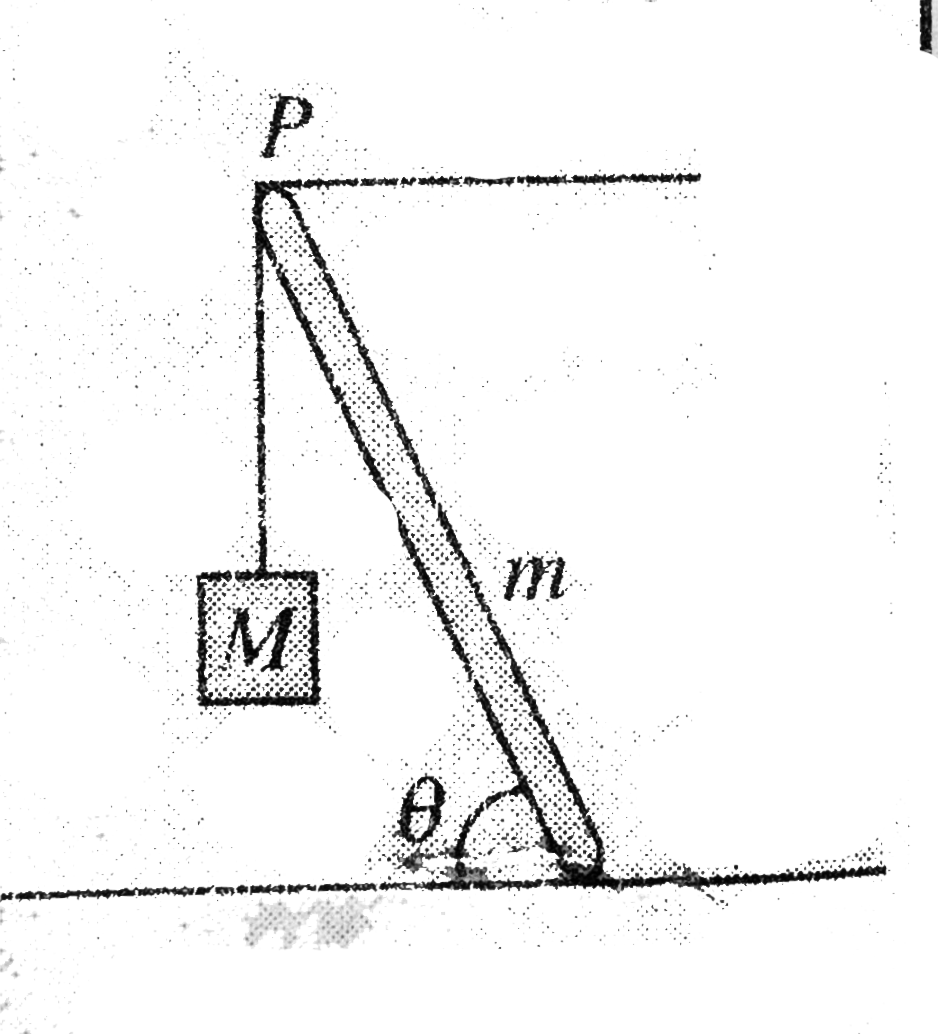 .
.
View Solution
