
The quarter disc of radius R (see figure) has a uniform surface charge density σ.
(a) Find electric potential at a point (O,O,Z)
(b). Find the Z component of electrif field at (O,O,Z)
σ8ε0[1−Z√R2+Z2]
σ4ε0[(√R2+Z2)+Z]
σ8ε0[√R2+Z2−Z]
σ8ε0[Z√R2+Z2]
The correct Answer is:C
Step by step video & image solution for The quarter disc of radius R (see figure) has a uniform surface charge density sigma. (a) Find electric potential at a point (O,O,Z) (b). Find the Z component of electrif field at (O,O,Z) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
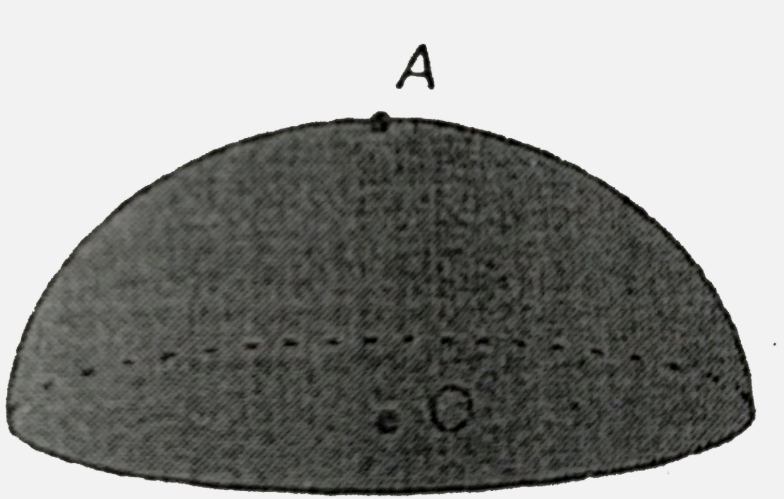
A hemispherical bowl of radius R carries a uniform surface charge density σ. Find the potential at the topmost point A, taking potential at infinity to be zero.
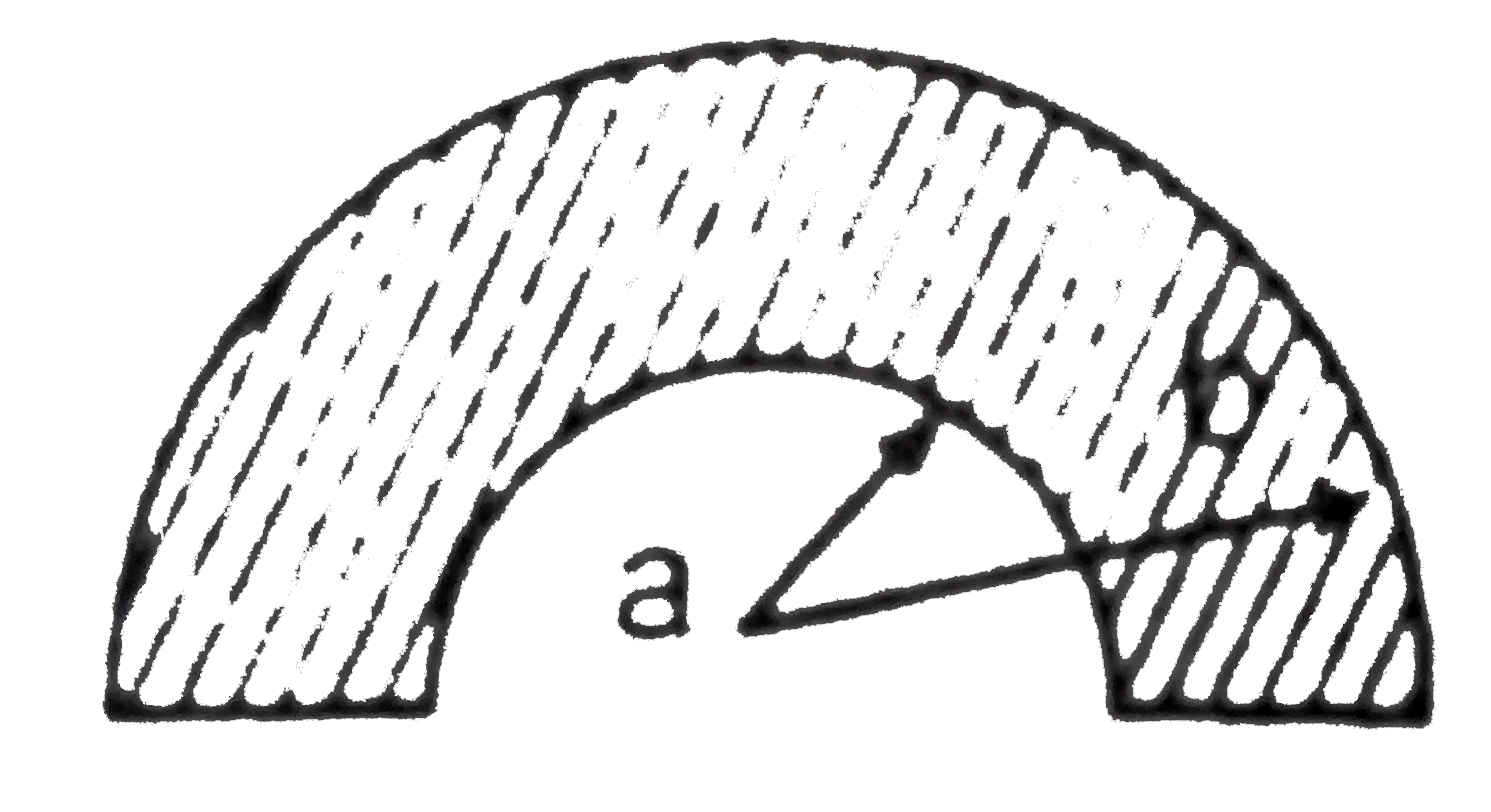
View SolutionA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
View Solution
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
A solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnetude) at point 'C' inside the cavity
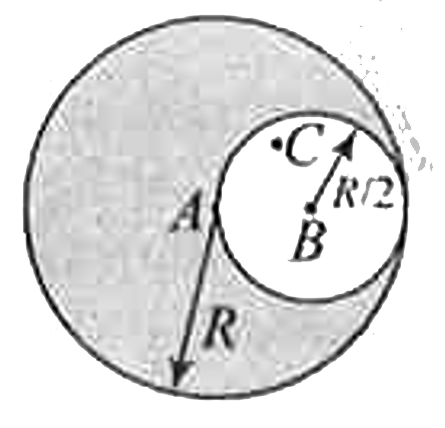
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View SolutionAn annular disc of inner radius a and outer radius '2a' is uniformly charged with uniform surface charge density σ. Find the potential at a distance 'a' from the centre at a point 'P' lying on the axis.
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
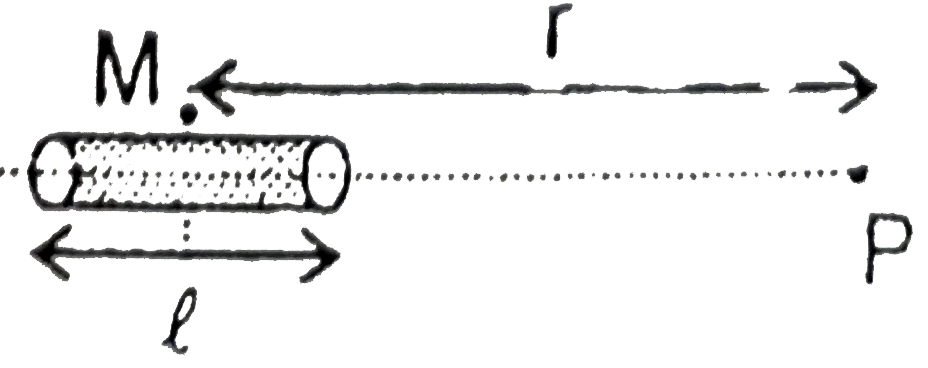
View SolutionA insulating cylindrical rod of diameter d and length l(l>>d) has a uniform surface charge density such that the electric field just outside the curved surface of the cylinder at point M is E0. Find the electric field due to charge distribuition at point P(r>>l).
View SolutionTwo infinite, non-conducting sheets of charge are parallel to each other, as shown in figure. The sheet on the left has a uniform surface charge density σ, and the one on the right has a uniform charge density −σ. Calculate the electric field at points (a) to the left of, (b) in between, and (c) to the right of the two sheets.

View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending up to infinity in the first quadrant of x−y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the point (0,0,d) and (0,0,2d)
View Solution
