Concentric metallic hollow spheres of radii R and 4R hold charges Q1andQ2 respectively. Given that surface charge densities of the concentric spheres are equal, the potential difference V(R)−V(4R) is :
3Q24πε0R
3Q116πε0R
Q24πε0R
3Q14πε0R
To solve the problem of finding the potential difference V(R)−V(4R) between two concentric metallic hollow spheres with radii R and 4R that hold charges Q1 and Q2 respectively, and given that their surface charge densities are equal, we can follow these steps:
1. Understand Surface Charge Density:
The surface charge density σ is given by:
σ=QA
where A is the surface area. For a sphere, A=4πr2. Therefore, for the inner sphere:
σ1=Q14πR2
and for the outer sphere:
σ2=Q24π(4R)2=Q264πR2
Since σ1=σ2, we have:
Q14πR2=Q264πR2
This simplifies to:
Q1=Q216
2. Calculate the Potential at R:
The potential V(R) at the surface of the inner sphere due to its own charge Q1 is:
V(R)=kQ1R+kQ24R
where k=14πϵ0.
3. Calculate the Potential at 4R:
The potential V(4R) at the surface of the outer sphere due to its own charge Q2 is:
V(4R)=kQ24R+kQ14R
4. Find the Potential Difference:
Now, we find the potential difference:
V(R)−V(4R)=(kQ1R+kQ24R)−(kQ24R+kQ14R)
The kQ24R terms cancel out:
V(R)−V(4R)=kQ1R−kQ14R=kQ1(1R−14R)
Simplifying gives:
V(R)−V(4R)=kQ1(4−14R)=kQ134R
5. Substituting k:
Substitute k=14πϵ0:
V(R)−V(4R)=34⋅14πϵ0⋅Q1R=3Q116πϵ0R
Final Result:
Thus, the potential difference V(R)−V(4R) is:
3Q116πϵ0R
The surface charge density σ is given by:
σ=QA
where A is the surface area. For a sphere, A=4πr2. Therefore, for the inner sphere:
σ1=Q14πR2
and for the outer sphere:
σ2=Q24π(4R)2=Q264πR2
Since σ1=σ2, we have:
Q14πR2=Q264πR2
This simplifies to:
Q1=Q216
The potential V(R) at the surface of the inner sphere due to its own charge Q1 is:
V(R)=kQ1R+kQ24R
where k=14πϵ0.
The potential V(4R) at the surface of the outer sphere due to its own charge Q2 is:
V(4R)=kQ24R+kQ14R
Now, we find the potential difference:
V(R)−V(4R)=(kQ1R+kQ24R)−(kQ24R+kQ14R)
The kQ24R terms cancel out:
V(R)−V(4R)=kQ1R−kQ14R=kQ1(1R−14R)
Simplifying gives:
V(R)−V(4R)=kQ1(4−14R)=kQ134R
Substitute k=14πϵ0:
V(R)−V(4R)=34⋅14πϵ0⋅Q1R=3Q116πϵ0R
Thus, the potential difference V(R)−V(4R) is:
3Q116πϵ0R
Topper's Solved these Questions
Similar Questions
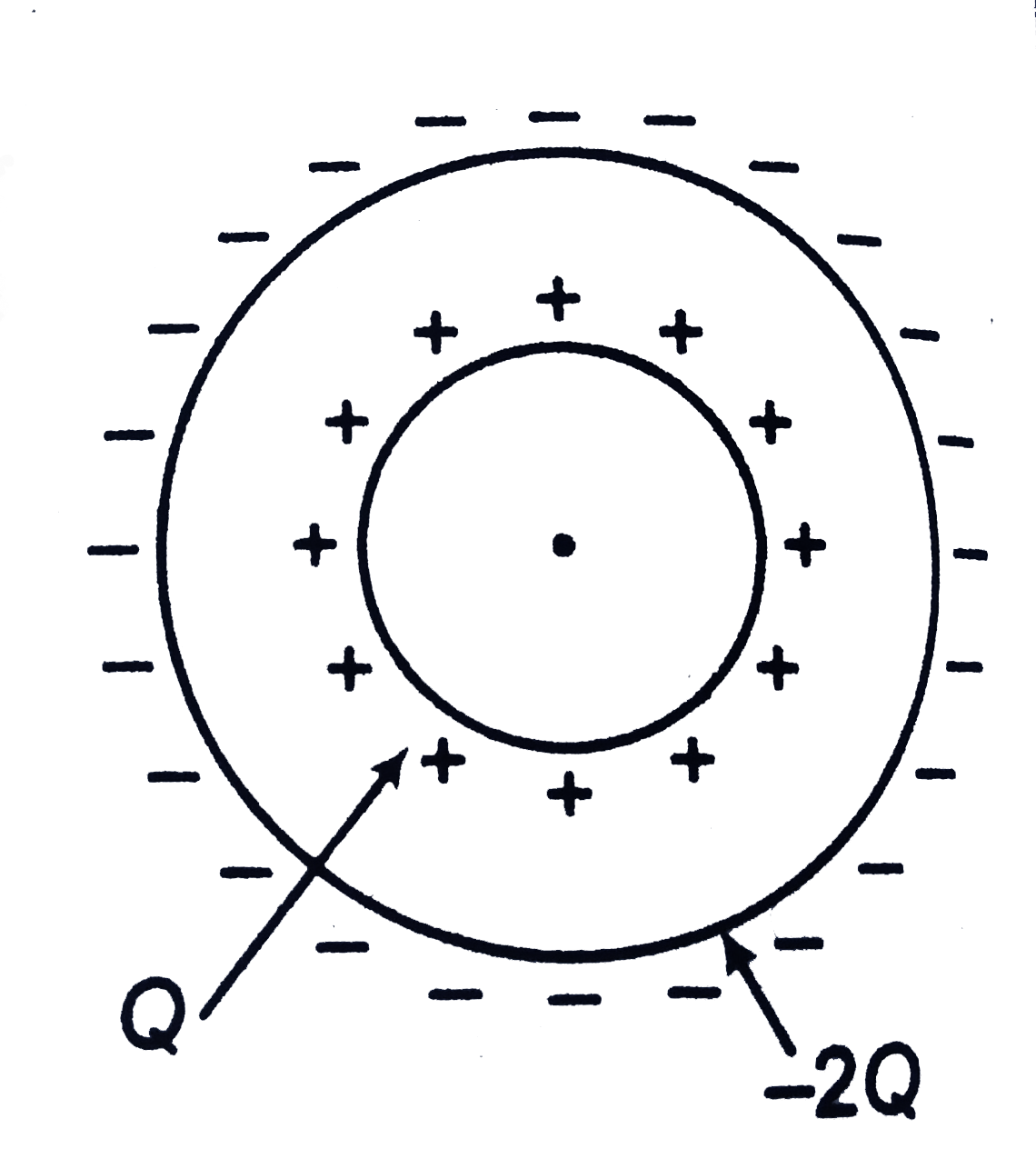
Two concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionThree concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo concentric spheres of radii R and r have similar charges with equal surface charge densities (σ). The electric potential at their common centre is
View SolutionTwo connectric spheres of radii R and r have similar charges with equal surface charge densities (sigam). The electric potential at their common centre is
View SolutionTwo isolated metallic spheres of radii 2 cm and 4 cm are given equal charge, then the ratio of charge density on the surfaces of the spheres will be
View SolutionA hollow metal sphere of radius 5cm is charged so that the potential on its surface is 10V. The potential at the centre of the sphere is
View SolutionA charge Q is distributed over two concentric hollow spheres of radii r and R(>r) such that the surface charge densities are equal. Find the potential at the common centre.
View Solution