AB and AC are the two tangets to a circle whose radius is 6cm. If ∠BAC=60∘, then what is the value (in cm) of √(AB2+AC2)?
6√6
4√6
9√3
8√3
Step by step video & image solution for AB and AC are the two tangets to a circle whose radius is 6cm. If angleBAC=60^(@), then what is the value (in cm) of sqrt((AB^(2)+AC^(2)))? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
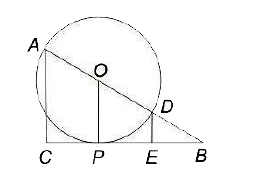
In the given figure, AC and DE are perpendicular to tangent CB.AB passess through centre O of the circle whose radius is 20 cm. If AC=36 cm, what is the length (in cm) of DE?
View SolutionAP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then the length of AP (in cm) is
View Solution
Knowledge Check
AB and AC are the two tangents to a circle whose radius is 6 cm. If ∠BAC=60∘ , then what is the value (in cm) of √(AB2+AC2)?
A6√6B4√6C9√3D8√3AB and AC are the two tangets to a circle whose radius is 6cm. If ∠BAC=60∘, then what is the value (in cm) of √(AB2+AC2)?
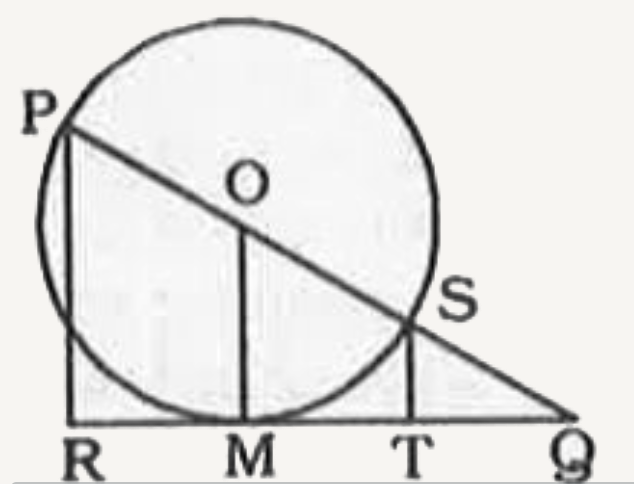
A6√6B4√6C9√3D8√3In the given figure ,PR and ST are perpendiculars to tan- gent QR, PQ passes through centre O of the circle whose diameter is 10 cm . If PR = 9 cm what is the length (in cm.) of ST ?
 A4B6C2D8
A4B6C2D8
AB and AC are two chords of a circle of radius r such that AB=2AC. If p and q are the distances of AB and AC from the centre Prove that 4q2=p2+3r2.
View SolutionIn a circle of radius 5cm, AB and AC are two chords such that AB=AC=8 cm. What is the length of chord BC?
View SolutionIn the given figure ,PR and ST are perpendiculars to tan- gent QR, PQ passes through centre O of the circle whose diameter is 10 cm . If PR = 9 cm what is the length (in cm.) of ST ?

View SolutionLength of two chords AB and AC of a circle are respectively 8 cm and 6 cm and ∠BAC=90∘. What is the radius of the circle?
View SolutionThere is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
View Solution
