The point of intersection for the diagonals AC and BD of the cyclic quadrilateral ABC is P. If ∠APB=64∘ and ∠CBD=28∘, the measure of ∠ADB is
56∘
28∘
32∘
36∘
Step by step video & image solution for The point of intersection for the diagonals AC and BD of the cyclic quadrilateral ABC is P. If angleAPB=64^(@) and angleCBD=28^(@), the measure of angleADB is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The point of intersection for the diagonals AC and BD of the cyclic quadrilateral ABC is P. If ∠APB=64∘ and ∠CBD=28∘, the measure of ∠ADB is
A32∘B36∘C56∘D28∘ABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If ∠APB=110∘ and ∠CBD=30∘, then ∠ADB measures
A55∘B30∘C70∘D80∘ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is:
Aa) 50∘Bb) 35∘Cc) 55∘Dd) 30∘
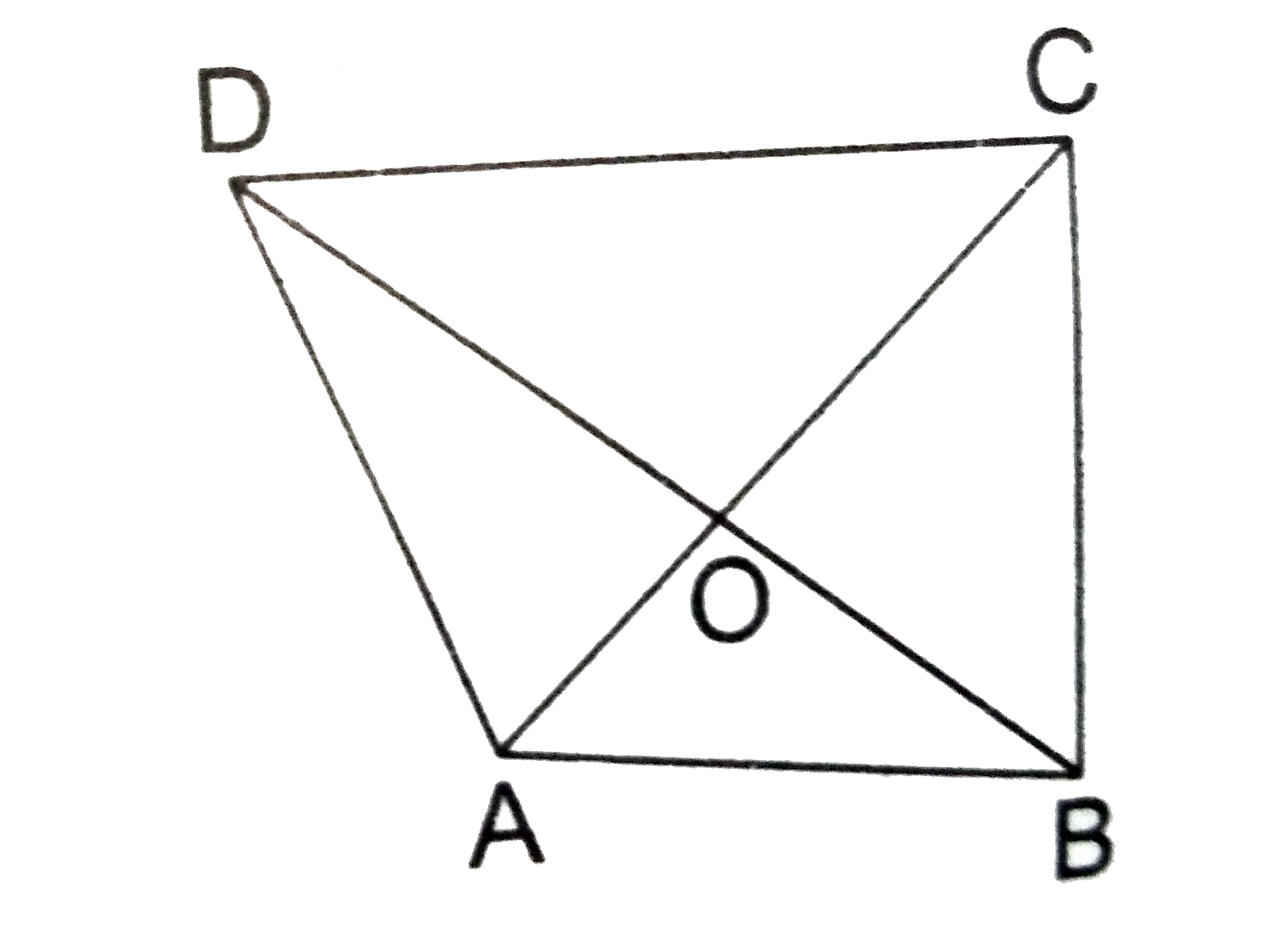
In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
View SolutionThe diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that
View SolutionThe diagonals AC and BD of a cyclic quadrilateral ABCD inter sect each other at the point P. Then, it is always true that
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
View SolutionABCD is a cycle quadrilateral. Diagonals BD and AC intersect each other at E. If ∠BEC=128∘ and ∠ECD=25∘ then what is the measure of ∠BAC ?
View Solution