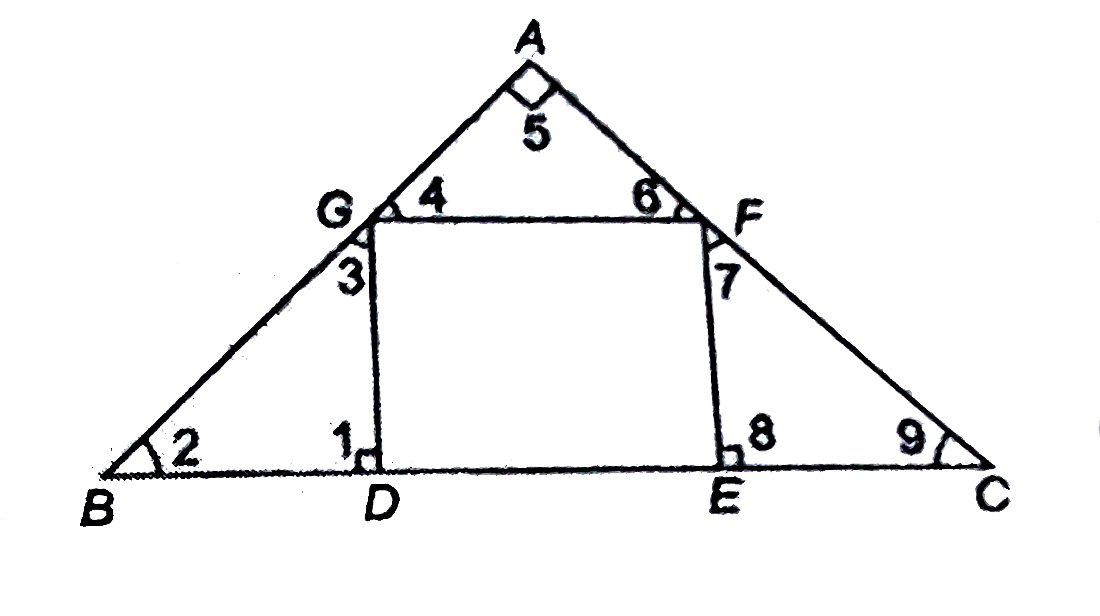
In the given figure , DEFG is a square and ∠BAC=90∘
prove that
(i) △AGF~△DBG
(ii)△AGF~△EFC
(iii) △DBG~△EFC
(iv) DE2=BD×EC
Step by step video & image solution for In the given figure , DEFG is a square and angleBAC= 90^(@) prove that (i) triangleAGF~ triangleDBG (ii) triangleAGF~triangleEFC (iii) triangleDBG ~ triangleEFC (iv) DE^(2)= BD xx EC by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
In the given figure DEFG is a square and ∠BAC=90∘ . Show that FG2=BG×FC .
 View Solution
View SolutionIn the given figure, DEFG is a square and ∠BAC=90∘, Prove that
(i)ΔAGF~ΔDBG
(ii) ΔAGF~ΔEFC
(iii)DE2=BD×EC
 View Solution
View SolutionIn the given figure if ∠B=90∘ and BD is perpendicular to AC then
prove that:
(i)△ADB~△BDC(ii)△ADB~△ABC
(iii) △BDC~△ABC(iv)BD2=AD×DC
(v) AB2=AD×AC(vi)BC2=CD×AC
(vii) AB2+BC2=AC2
 View Solution
View SolutionIn fig.7.84, DEFG is a square and ∠BAC=90°. Prove that:
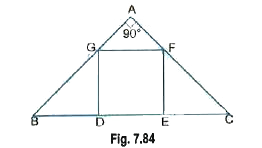
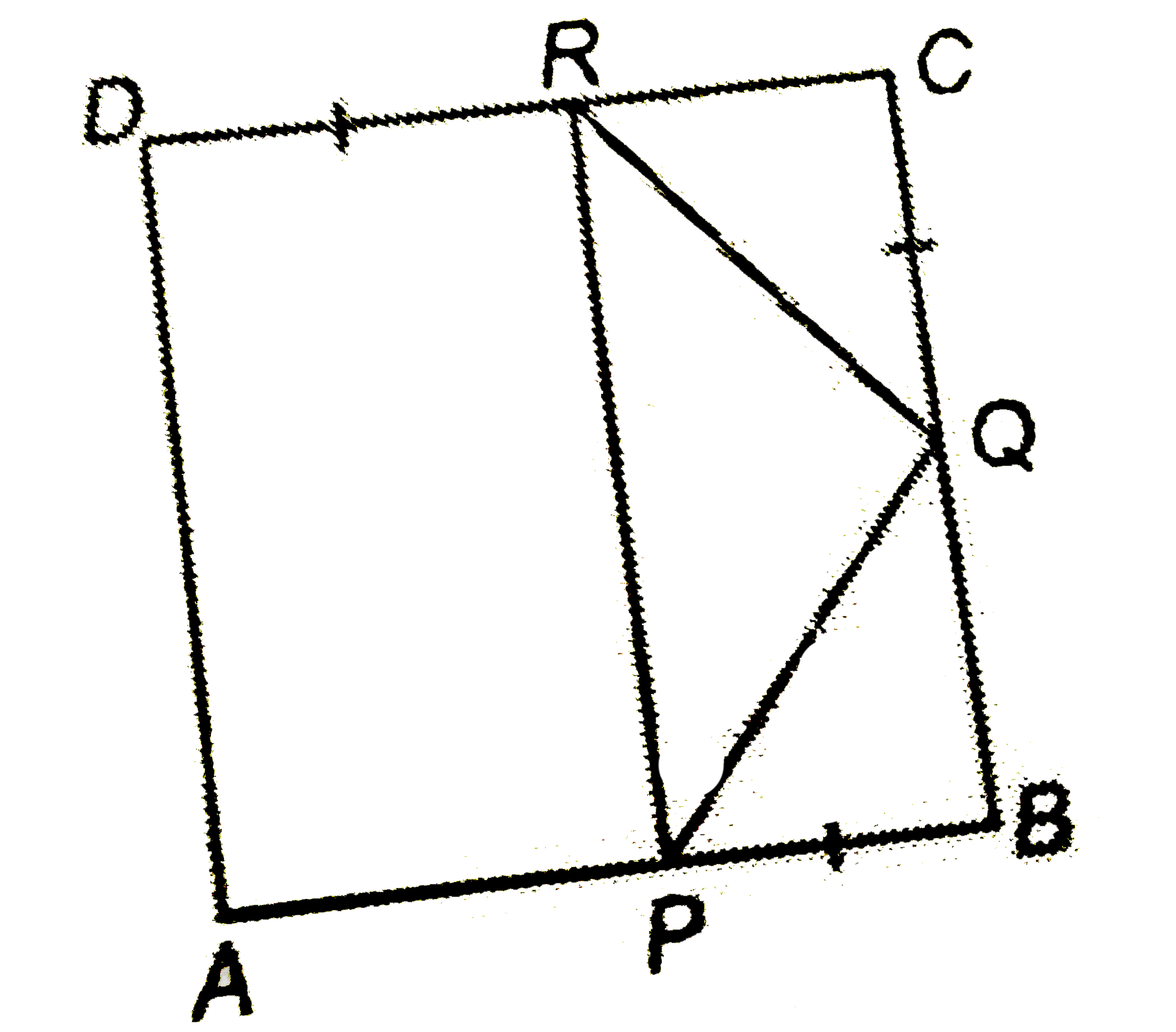
(i) ΔAGF~ΔDBG (ii) ΔAGF~ΔEFC(iii) ΔDBG~ΔEFC (iv) DE2=BD×ECView SolutionIn the given figure, ABCD is a square and ∠PQR=90∘.IfPB=QC=DR, prove that.
(i) QB = RC
(ii) PQ = QR
(iii) ∠QPR=45∘
 View Solution
View SolutionIn the given figure, ∠ACB=90∘andCD⊥AB. Prove that CD2=BD⋅AD
 View Solution
View SolutionIn the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.
 View Solution
View SolutionIn the given figure, AD = AE and AD2=BD×EC prove that: triangles ABD and CAE are similar.
View SolutionIn the given figure, AB||DC and ∠D=∠C. Prove that :
(i) AD=BC
(ii) AC=BD
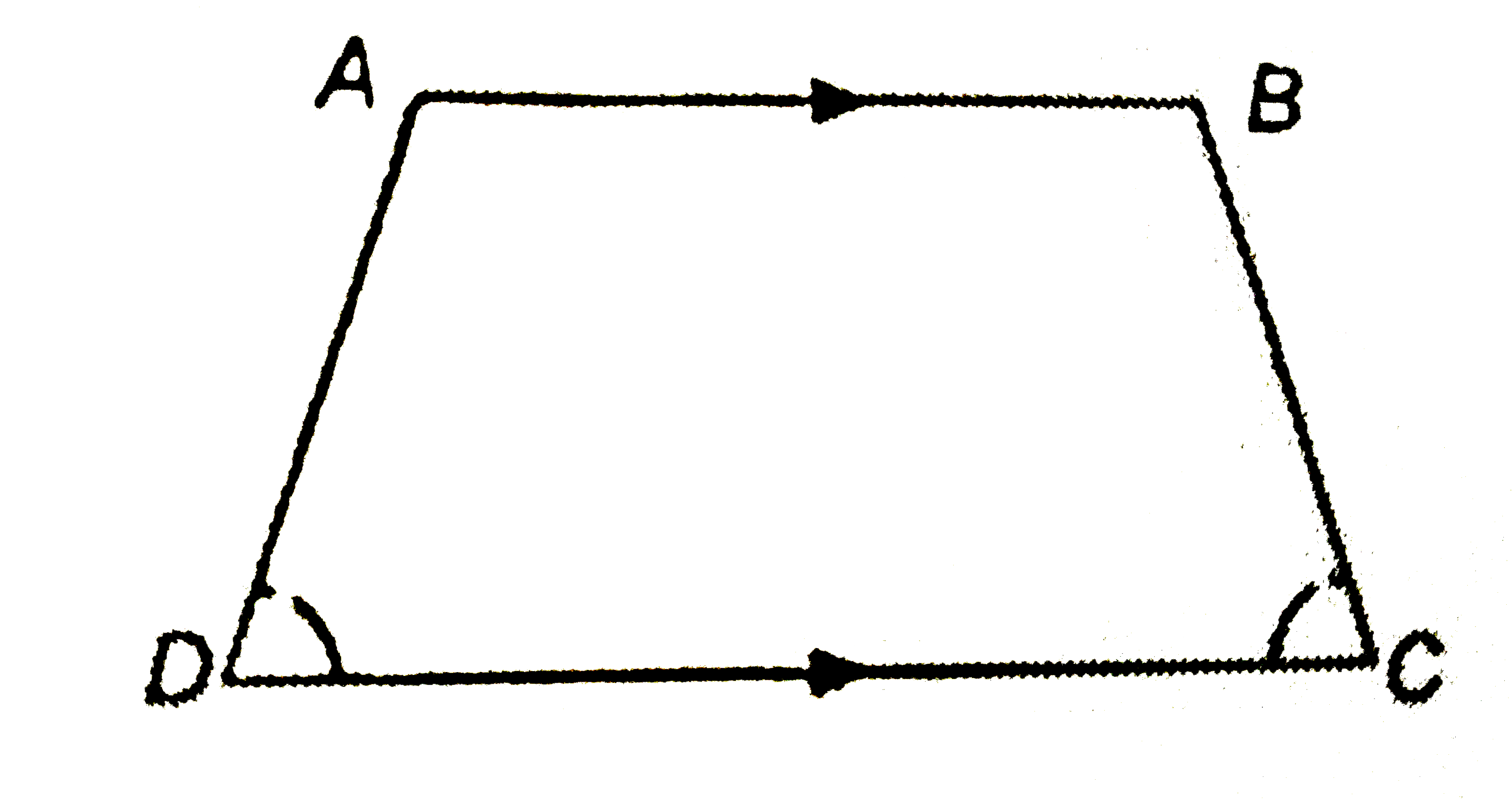 View Solution
View SolutionIn the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP
 View Solution
View Solution

