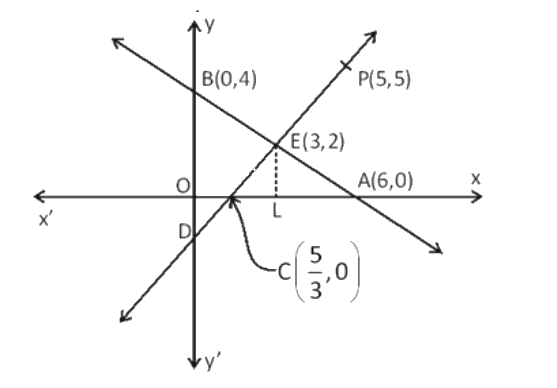
The line 2x+3y=12 meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
Step by step video & image solution for The line 2x+3y=12 meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
View SolutionThe line xa+yb=1 meets the axis of and y at A and B respectively and C is middle point of AB then
View Solution
Knowledge Check
The line xa−yb=1 cuts the x-axis at P. The equation of the line through P and perpendicular to the given line is
A(a) x+y=abB(b) x+y=a+bC(c) ax+by=a2D(d) bx+ay=b2
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, 5) is the mid-point of PQ, then find the coordinates of P and Q.
View SolutionThe line 3x - 4y + 12 = 0 meets x-axis at point A and y-axis at point B. Find :
equation of perpendicular bisector of line segment AB
View SolutionA line cuts the x-axis at A(7,0) and the y-axis at B(0,−5) A variable line PQ is drawn perpendicular to AB cutting the x-axis in P and the y-axis in Q. If AQ and BP intersect at R, find the locus of R.
View SolutionA line intersects the Y- axis and X-axis at the points P and Q, respectively. If (2,-5) is the mid- point of PQ, then the coordinates of P and Q are, respectively.
View SolutionThe line 3x - 4y + 12 = 0 meets x-axis at point A and y-axis at point B. Find :
the co-ordinates of A and B.
View SolutionThe straight line 2x+3y=24 meets the x-axis at P and the y-axis at Q. The perpendicular bisector of PQ meets the line through (-2,0) parallel to the y-axis at R. Find the area of the ΔPQR.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
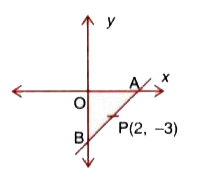
equation of line AB.
View Solution