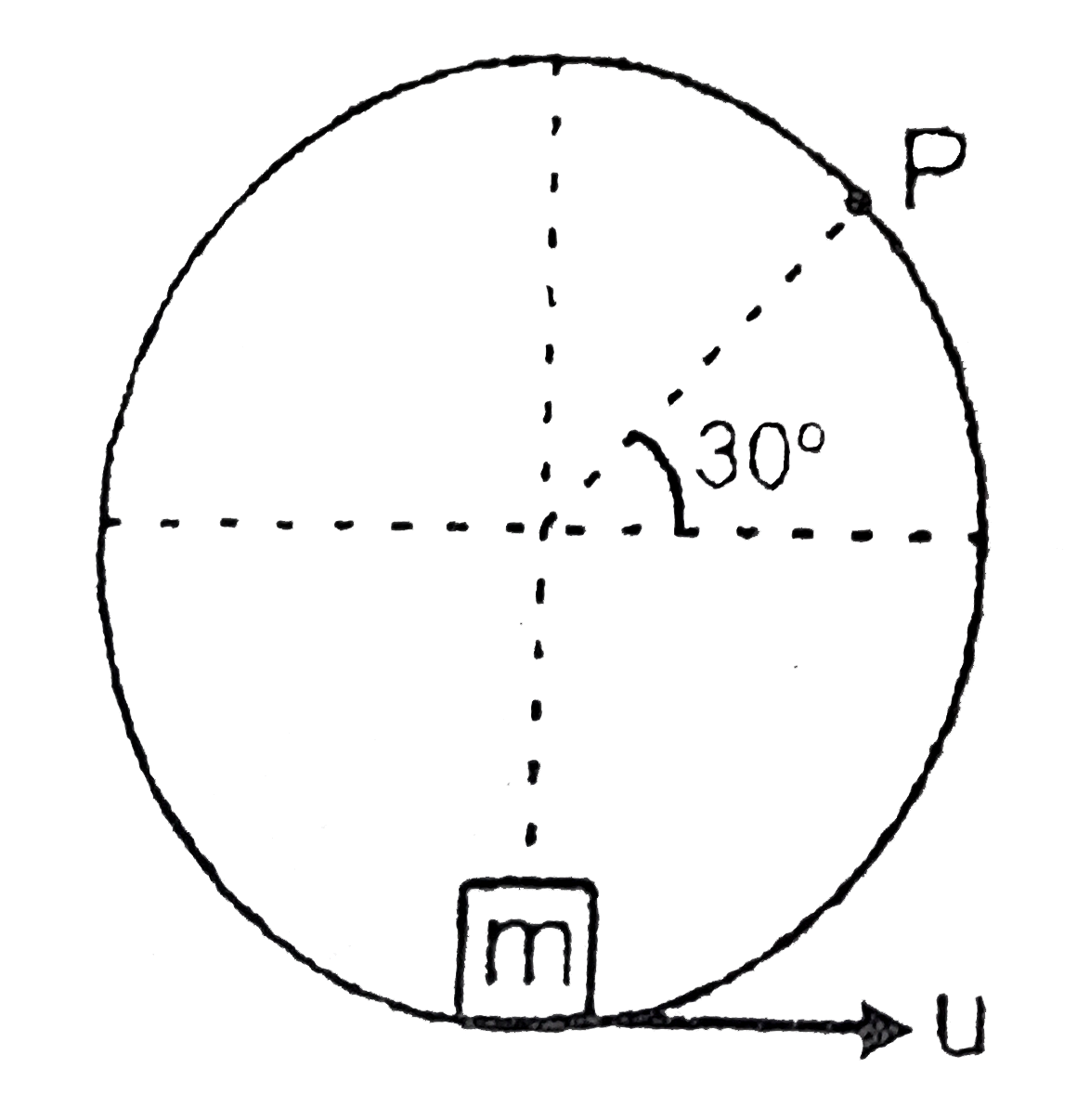
A hollow vertical cylinder of radius R and height h has smooth internal surface. A small particle is placed in contact with the inner side of the upper rim at a point P. It is given a horizontal speed V0 tangential to rim. It leaves the lower rim at point Q, vertically below P. The number of revolutions made by the particle will be:
To solve the problem of finding the number of revolutions made by a particle in a hollow vertical cylinder, we can follow these steps:
Step 1: Understand the motion of the particle
The particle is given an initial horizontal speed V0 at the top of the cylinder. It will fall vertically due to gravity while moving horizontally. The vertical distance it will fall is equal to the height of the cylinder h.
Step 2: Calculate the time taken to fall
Using the kinematic equation for vertical motion, we can find the time t it takes for the particle to fall a distance h:
Sy=Uy⋅t+12Ay⋅t2
Where:
- Sy=h (the height of the cylinder)
- Uy=0 (initial vertical velocity)
- Ay=g (acceleration due to gravity)
Substituting these values, we get:
h=0⋅t+12gt2
This simplifies to:
h=12gt2
Rearranging gives:
t2=2hg⇒t=√2hg
Step 3: Calculate the horizontal distance traveled
The horizontal distance S traveled by the particle while it falls is given by:
S=V0⋅t
Substituting t from the previous step:
S=V0⋅√2hg
Step 4: Relate horizontal distance to the number of revolutions
The horizontal distance S can also be expressed in terms of the number of revolutions n and the circumference of the cylinder:
S=n⋅(2πR)
Where R is the radius of the cylinder. Setting the two expressions for S equal gives:
V0⋅√2hg=n⋅(2πR)
Step 5: Solve for the number of revolutions n
Rearranging the equation to solve for n:
n=V0⋅√2hg2πR
Final Answer
Thus, the number of revolutions made by the particle as it falls from point P to point Q is:
n=V02πR⋅√2hg
---
The particle is given an initial horizontal speed V0 at the top of the cylinder. It will fall vertically due to gravity while moving horizontally. The vertical distance it will fall is equal to the height of the cylinder h.
Using the kinematic equation for vertical motion, we can find the time t it takes for the particle to fall a distance h:
Sy=Uy⋅t+12Ay⋅t2
Where:
- Sy=h (the height of the cylinder)
- Uy=0 (initial vertical velocity)
- Ay=g (acceleration due to gravity)
h=0⋅t+12gt2
This simplifies to:
h=12gt2
Rearranging gives:
t2=2hg⇒t=√2hg
The horizontal distance S traveled by the particle while it falls is given by:
S=V0⋅t
Substituting t from the previous step:
S=V0⋅√2hg
The horizontal distance S can also be expressed in terms of the number of revolutions n and the circumference of the cylinder:
S=n⋅(2πR)
Where R is the radius of the cylinder. Setting the two expressions for S equal gives:
V0⋅√2hg=n⋅(2πR)
Rearranging the equation to solve for n:
n=V0⋅√2hg2πR
Thus, the number of revolutions made by the particle as it falls from point P to point Q is:
n=V02πR⋅√2hg
Similar Questions
A hollow vertical cylinder of radius R and height h has a smooth internal surface. A small particle is held in contact with the inner side of upper rim at a point P. It is given a horizontal speed v0 tangential to rim. It leaves the lower rim at point Q, vertically below P. The number of revolutions made by the particle will be [Take acceleration due to gravity g]
View Solution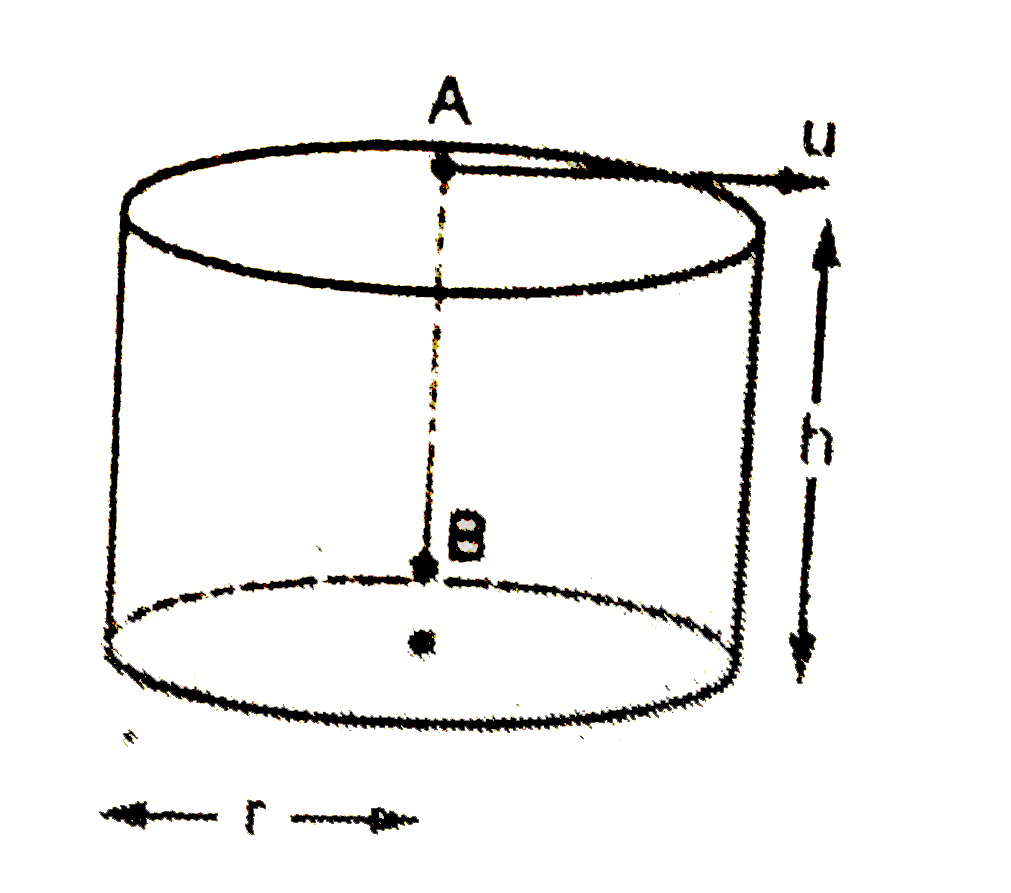
A hollow vertical cylinder of radius r and height h has a smooth internal surface. A small particle is placed in contact with the inner side of the upper rim, at point A, and given a horizontal speed u, tangentical t the rim. it leaves the lower rim at point B, vertically below A. If n is an integer then
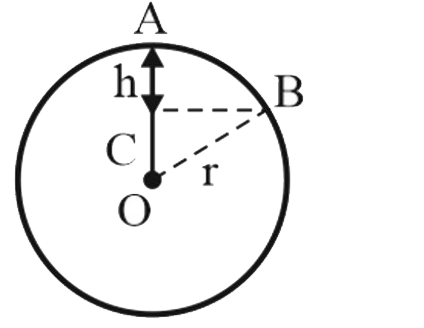
View SolutionIn figure, a particle is placed at the highest point A of a smooth sphere of radius r. It is given slight push, and it leaves the sphere at B, at a depth h vertically below A. The value of h is
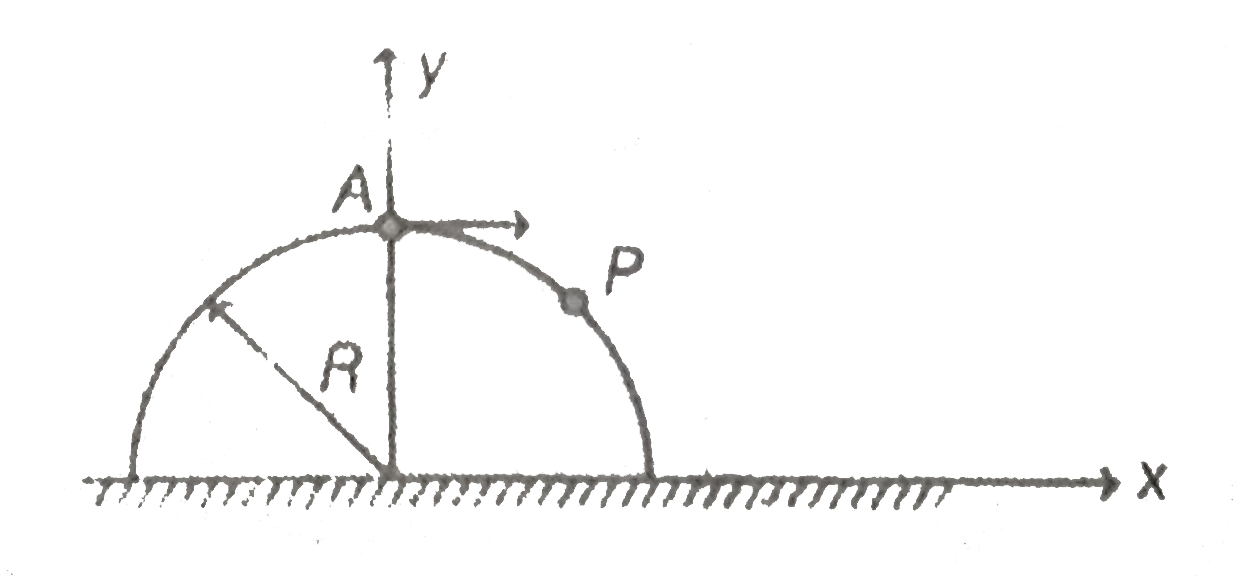
View SolutionA small particle is placed at the top point A of a fixed smooth hemisphere of radius R. Particle is given small displacement towards right and it starts slipping. Calculate velocity of the particle after hitting horizontal perfectly inelastic surface.
View SolutionA cylinder of radius R=1m and height H=3m two- thirds filled with water, is rotated about its vertical axis as shown in Fig. Determine the speed of rotation when
a. the: water just starts spilling over the rim.
b. the point at the centre of the base is just exposed.

View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
View SolutionA horizontal plane supports a fixed vertical cylinder of radius R and a particle is attached to the cylinder by a horizontal thread AB as shown in Fig. The particle initially rest on a horizontal plane. A horizontal velocity v0 is imparted to the particle, normal to the threading during subsequent motion. Point out the false statements:

View SolutionA small particle of mass m is fixed to the perimeter of a ring of same mass and radius r. The system comprising of particle and ring is placed on a horizontal plane. Friction is negligible on horizontal plane. Initially particle is at top most point, then the system is released from rest. Answer next two question when the particle is at the same height as the centre of ring aftr being released from top most point. Assume that the ring stays in vertical plane during its motion under consideration

Mark the CORRECT option(s):
View SolutionA uniform circular ring of mass m and radius R is placed freely on a horizontal smooth surface as shown in figure. A particle of mass m is connected to the circumference of the ring with massless string . The particle is imparted velocity v0 perpendicular to length of string as shown. If T is tension in the string just after the particle imparted velocity , then
Acceleration of point P at this instant , is
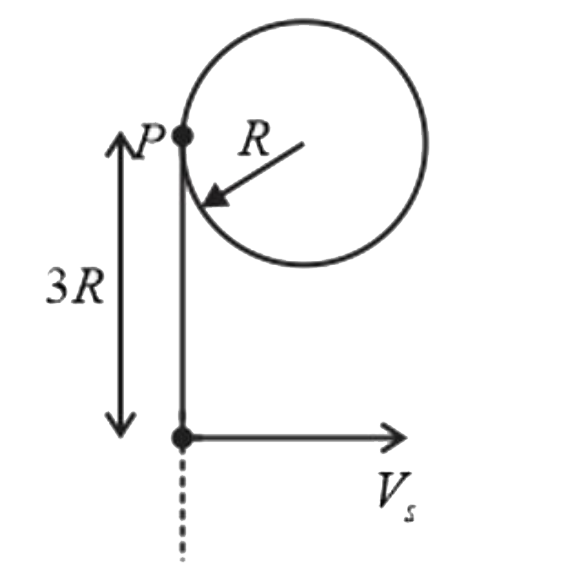
View SolutionA horizontal cylinder is fixed, its inner surface is smooth and its radius is R. A small block is initially at the lowest point. The minimum velocity that should by given to the block at the lowest point, so that it can just cross the point P is u then
View Solution
