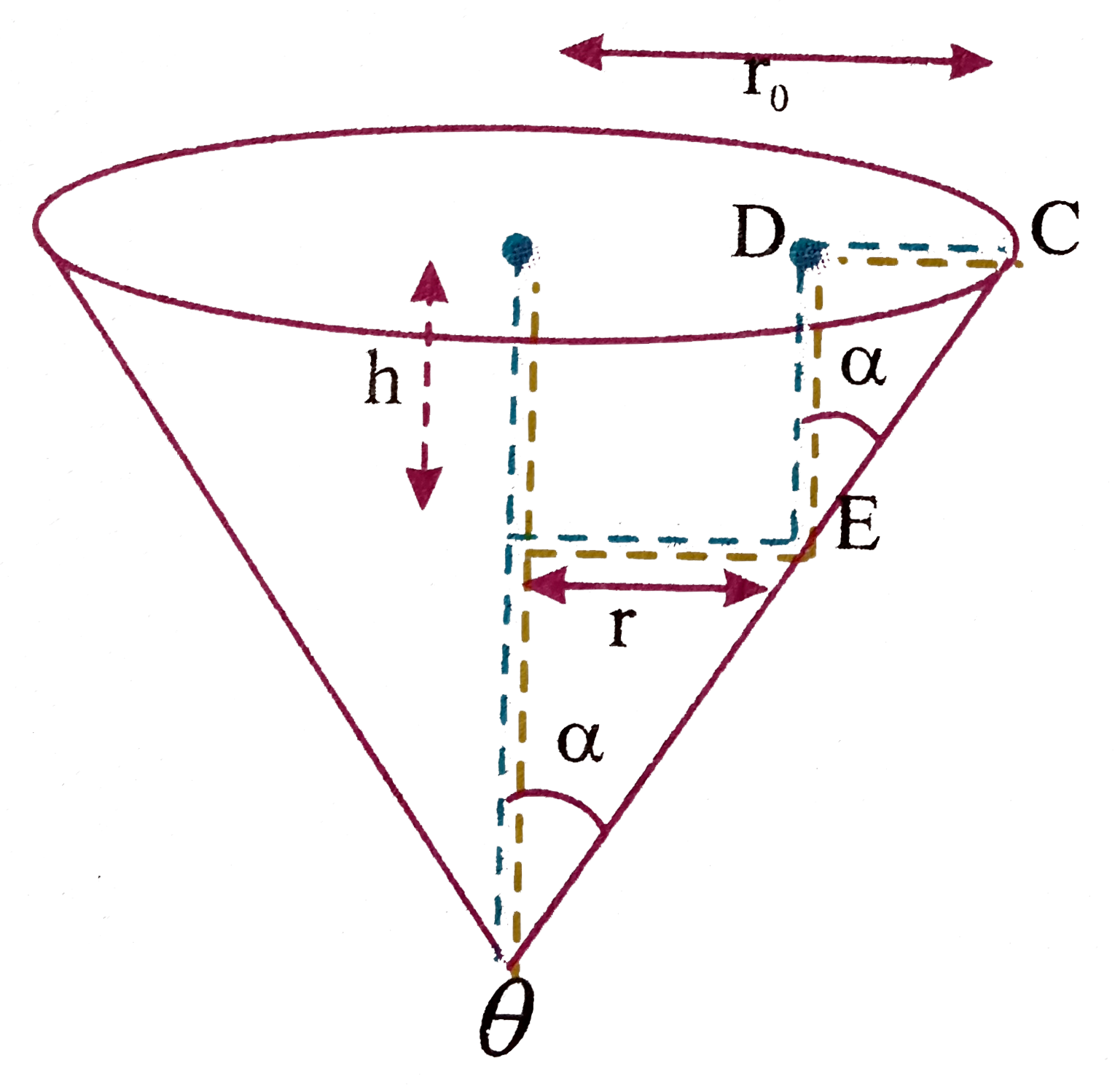
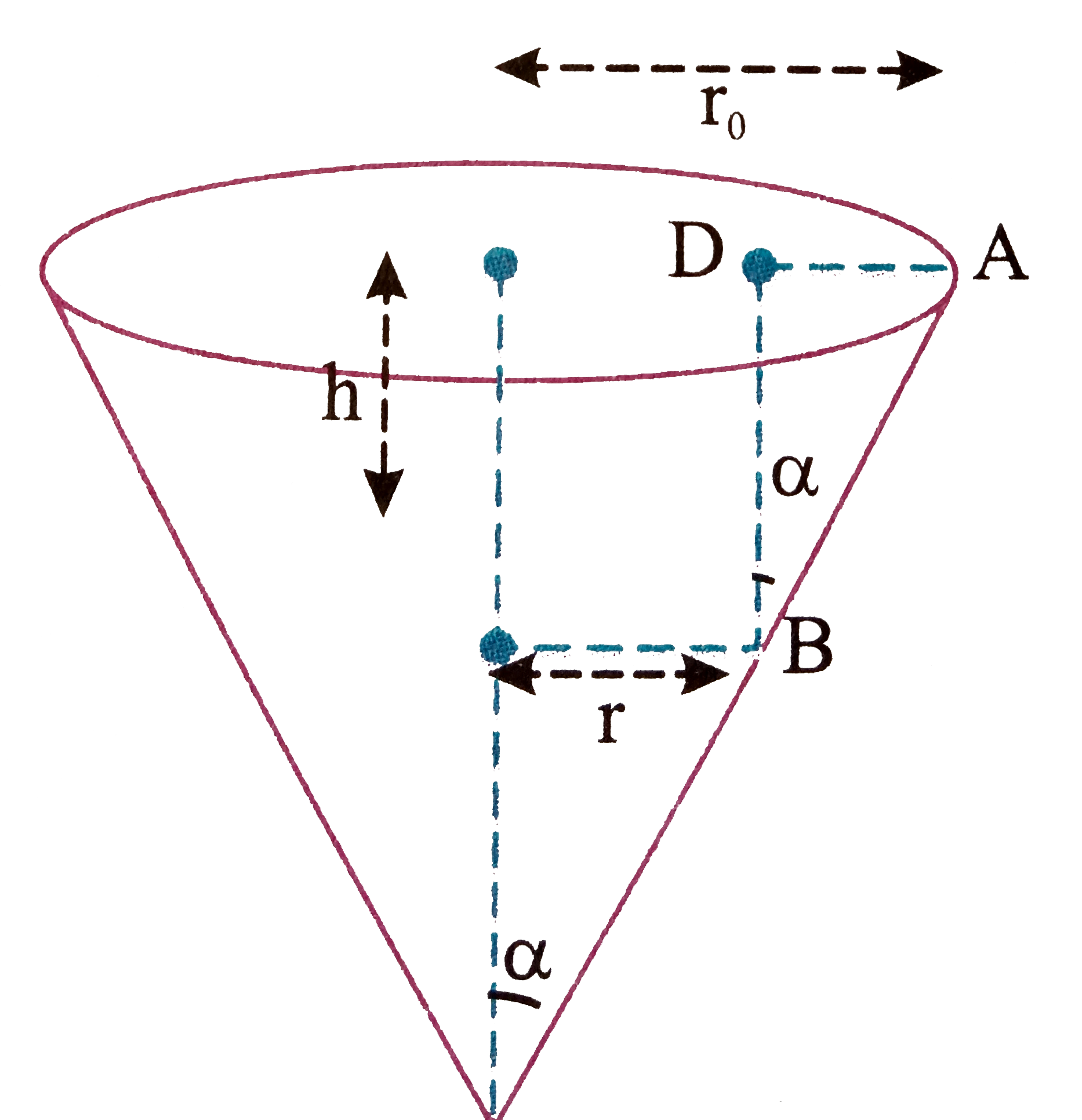
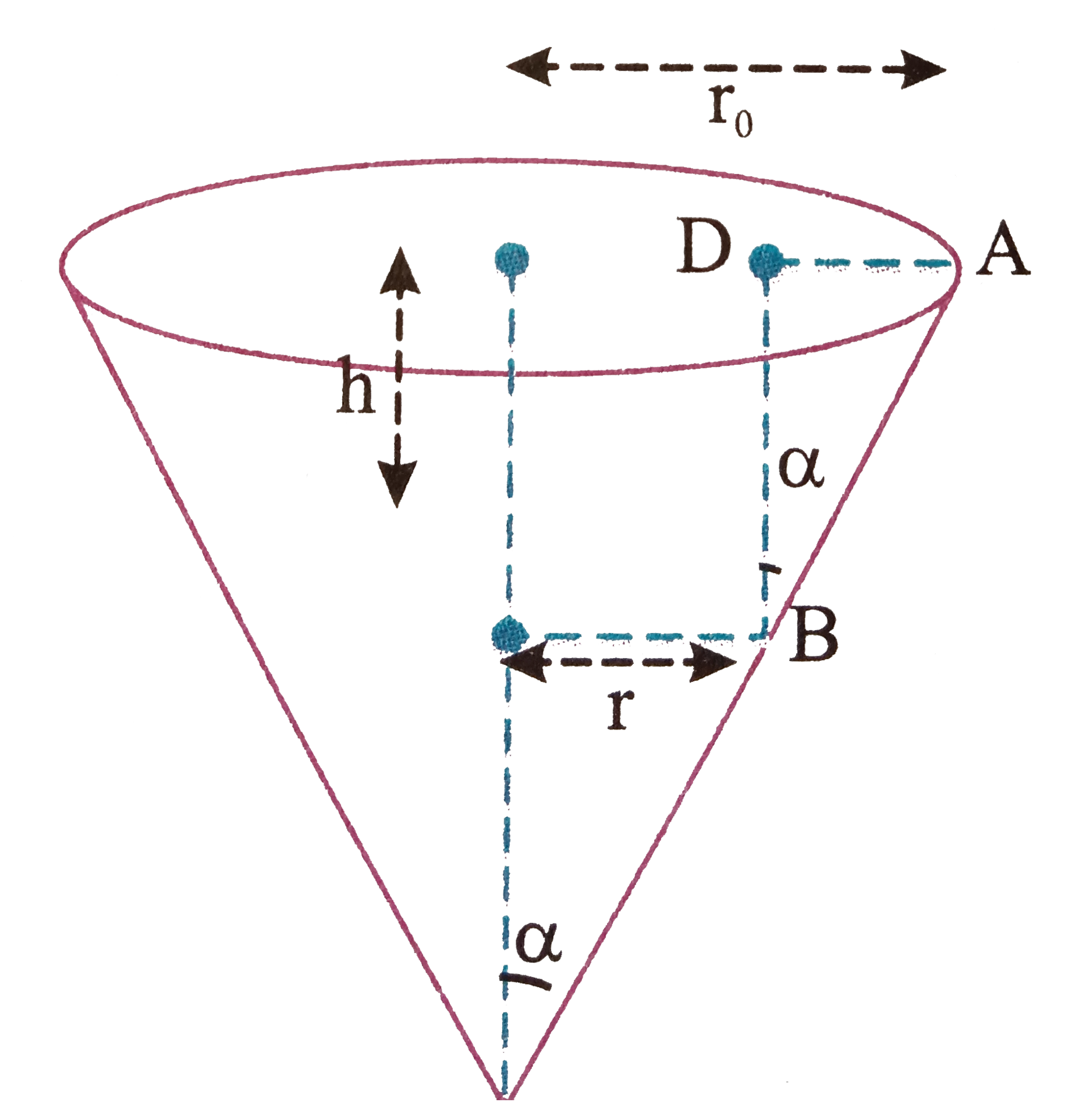
A small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The speed of particle at point B

√v20+2gh
√v20−2gh
√v20+gh
√2v20+2gh
The correct Answer is:A
From angular momentum conservation about axis of cone.
mv0r0=mvrcosθ
v0r0=vrcosθ.....(i)
from energy conservation E1=E2
12mv20+mgh=12mv2+0,v=√v20+2gh
r0−r=htanα,r=(r0−htanα)
From equations (i)
Eliminating v and substituting r=r0−htanα
v0r0=√v20+2gh(r0−htanα)cosθ
cosθ=v0r0√v20+2gh(r0−htanα)
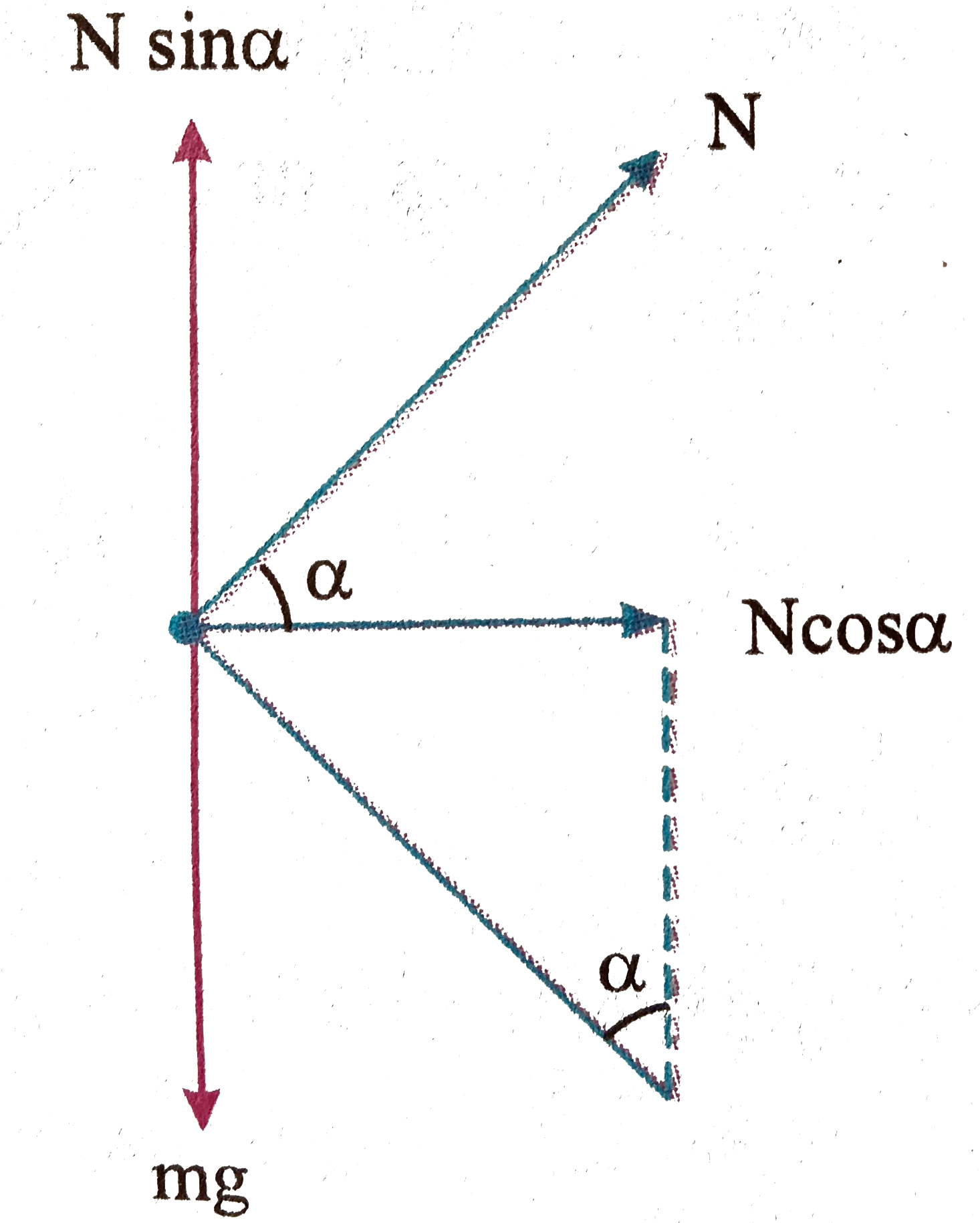
Nsinα=mg....(ii)Ncosα=mv20r0.....(iii)
Solving (ii) and (iii) tanα=gr0v20
J.a=IGω=112(3m)(4a2).ω=4ma2ω
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V72videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
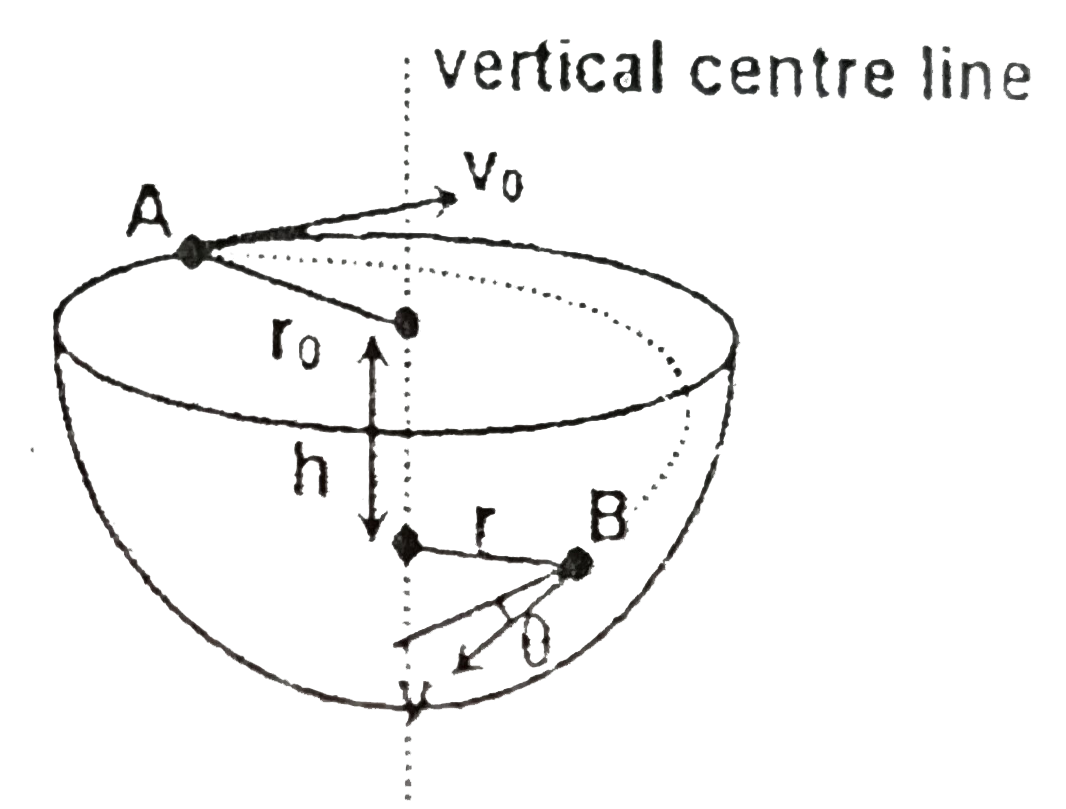
A small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemispherical bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the vertical centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.
 View Solution
View SolutionA small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The value of θ is
 Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2gh
Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2gh - Question 2 - Select One
A small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The minimum value of v0 for which particle will be moving in a horizontal circle of radius r0.
 A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanα
A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanα - Question 3 - Select One
A particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
AgcosθθvBgvsinθCgvθDgθvsinθ
A small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)
 View Solution
View SolutionA particle is thrown with an initial speed v0 at an angle α to the horizontal. Find the radius of curvature r at the highest point of its path, and its ratios to the maximum height H and to the distance L of the particle's flight.
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
View SolutionA particle of mass m is projected form ground with velocity u making angle θ with the vertical. The de Broglie wavelength of the particle at the highest point is
View Solution
