Question

Find the number of solutions of equation
$(2x-3)2^x=1$

Explanation

We have ` (2x - 3) 2^(x) = 1`
` or 2x-3 = 2^(-x) `
To find the number of roots of the above equation, we need to find the number of points of intersection of ` y = 2x - 3 and y = 2^(-x)`.
The graphs of functions are as shown in the following figure.

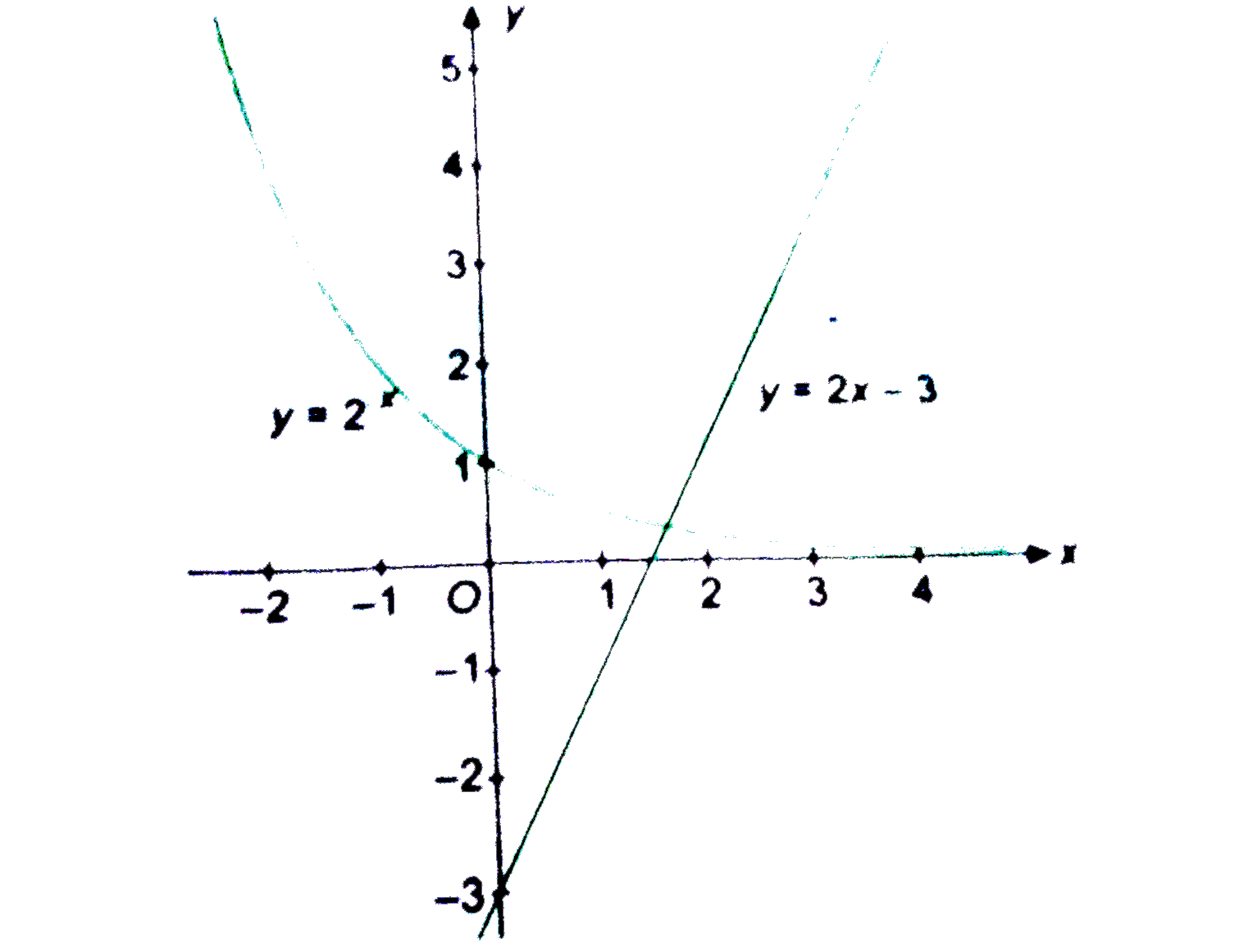
From the figure, graphs intersect at only one point.
Hence, there is only one solution of the given equation.