Find the number of solution to the equation sinx=x2+2x+1.
Let f(x) = sin x and g(x)=x2+2x+1=(x+1)2
Graphs of y = sin x and y=(x+1)2 are as shown in the following figure.
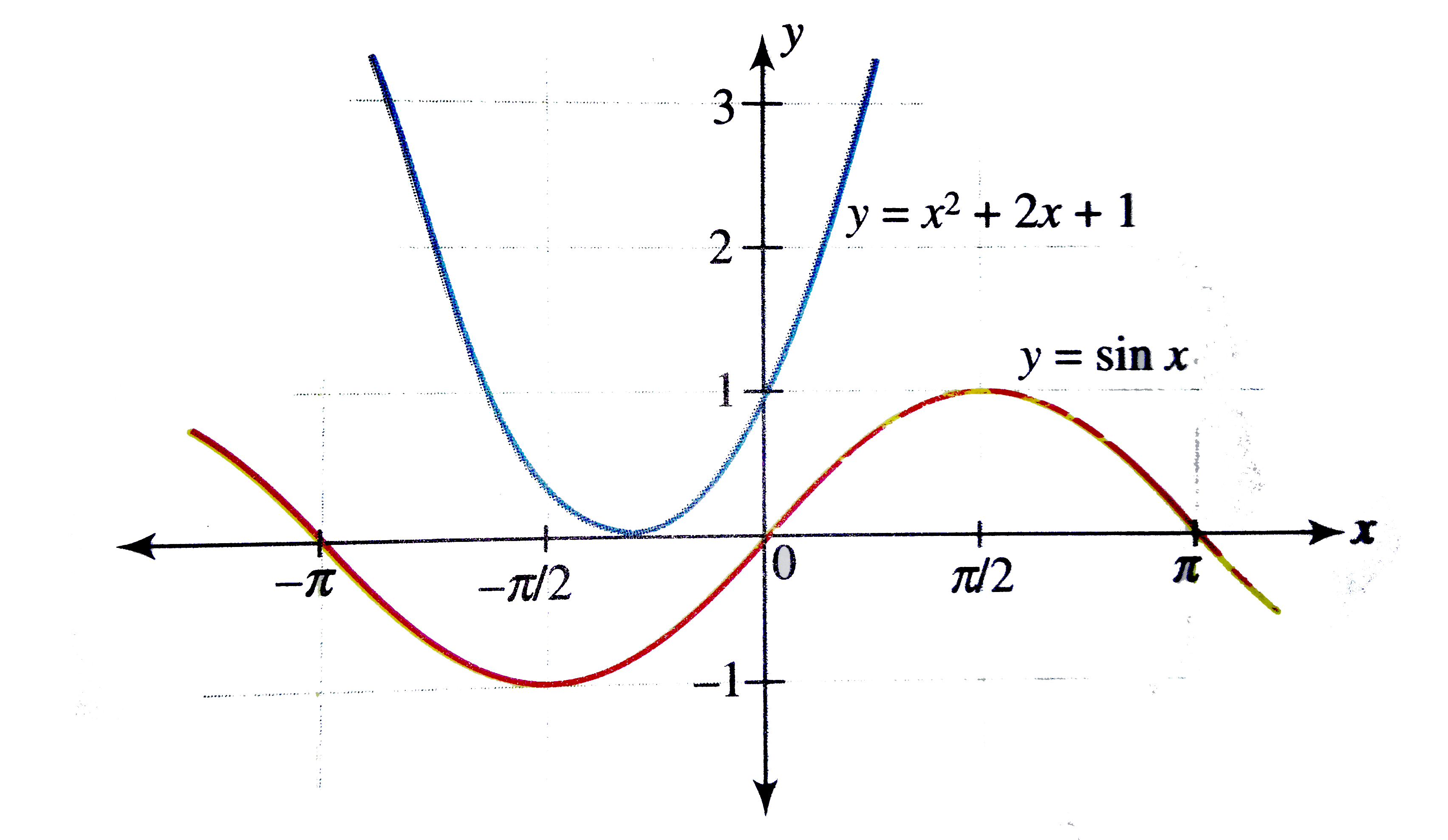
Since the curvey y=(x+1)2 meets the y - axis at (0, 1), it never intersects y = sin x. Hence no solution.
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Find the number of solutions of the equation sinx=x2+x+1.
View SolutionFind the number of solution of the equation sinx=x2+x+1.
View SolutionFind the number of solution of the equation sinx=x2+x+1.
View SolutionFind the number of solutions of the equation sinx=x2+x+1.
View SolutionFind the number of solutions of the equation sinx=x2+x+1.
View SolutionNumber of solution of equation sinx=x2+x+1 is
View SolutionFind the number of solutions of the equations
(sinx−1)3+(cosx−1)3+(sinx)3=(2sinx+cosx−2)3 in (0,2π).
View SolutionFind the number of solutions of the equations
(sinx−1)3+(cosx−1)3+(sinx)3=(2sinx+cosx−2)3 in (0,2π).
View SolutionFind the number of solutions of the equations
(sinx−1)3+(cosx−1)3+(sinx)3=(2sinx+cosx−2)3 in [0,2π].
View SolutionFind the number of solution of the equations
sin3xcosx+sin2x⋅cos2x+sinx⋅cos3x=1, when x∈[0,2π]
View Solution
