Write a possible rational function h with a hole at x = 5, a vertical asymptote at x = -1, a horizontal asymptote at y = 2 and x-intercept at x = 2.Solution in Tamil
The graph of f has a slant asymptote y=x+4 and a vertical asymptote at x=5 , hence f(x) may be written as f(x)=(x+4)+a(x−5),
where a is a constant to be determined using the fact that f(2)=0 since f has a zero at x=2.
f(2)=(2+4)+a2−5=0∴a=18
Hence f(x) is given by f(x)=(x+4)+18x−5=x2−x−2x−5
Check the characteristics of the graph of f shown below.
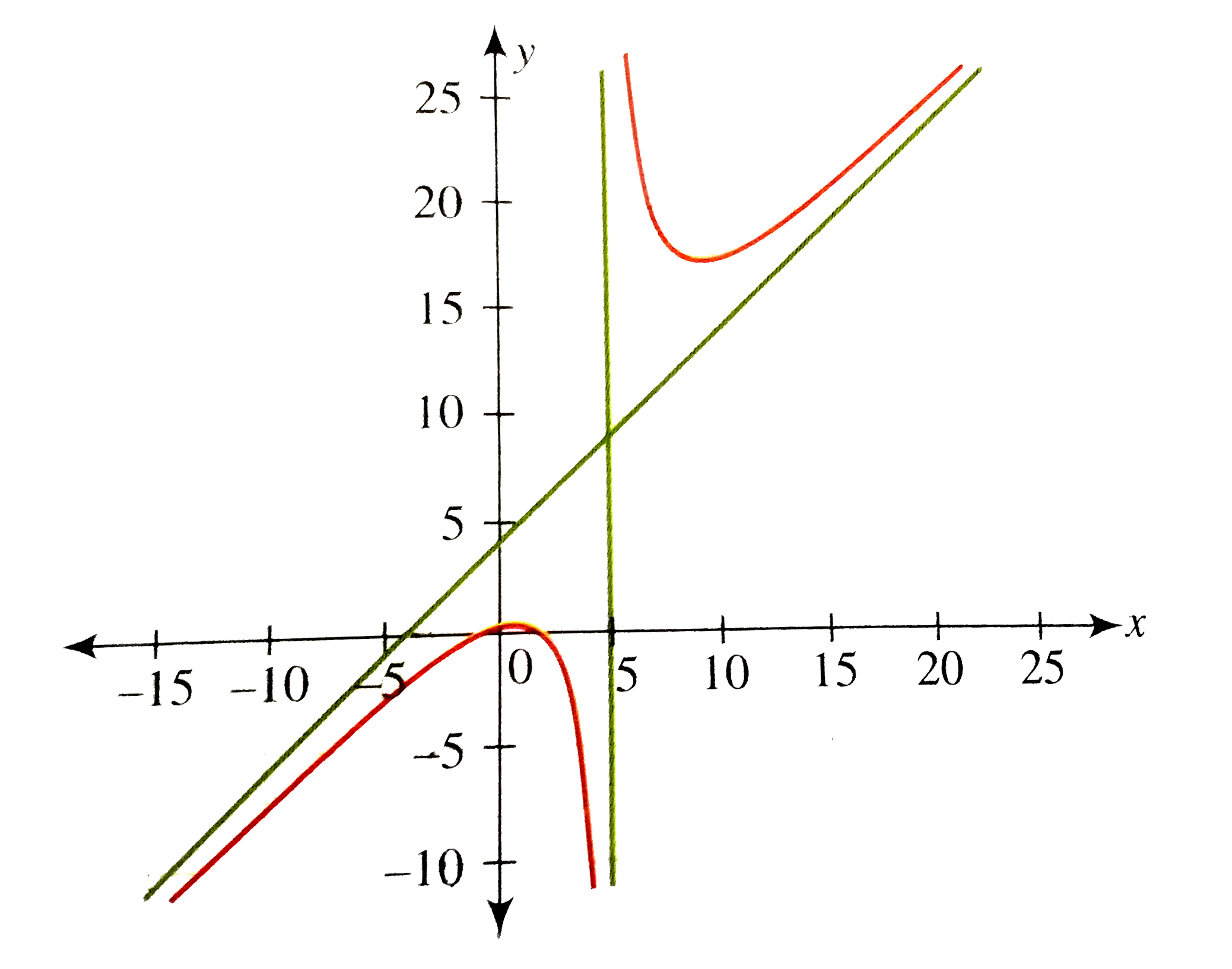
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise14videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
02:46View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=001:55View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionDraw the graph of y=1(1/x).
01:52View SolutionThe line x+y+1=0 is an asymptote of x2−y2+x−y−2=0. The other asymptote is
05:29View SolutionWrite a possible rational function h with a hole at x = 5, a vertical asymptote at x = -1, a horizontal asymptote at y = 2 and x-intercept at x = 2.
06:38View SolutionWrite a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept.
03:11View SolutionWrite a rational function f with a slant asymptote y=x+4, a vertical asymptote at x = 5 and one of the zeros at x = 2.
02:12View SolutionWrite a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.
06:36View SolutionThe line x+y+1=0 is an asymptote of x2−y2+x−y−2=0. The other asymptote is
01:18View SolutionWrite a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept.
01:38View SolutionWrite a rational function f with a slant asymptote y=x+4, a vertical asymptote at x = 5 and one of the zeros at x = 2.
01:07View SolutionWrite a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.
03:59View SolutionFind all the vertical asymptotes and holes of (x−3)2(x−4)(x−5)(x−3).
04:54View SolutionFind the vertical asymptotes and holes of x(x+5)4(x−2)6(x+5)6(x−2)3(x−5)
03:21View SolutionFind the vertical -asymptotes and holes of x2(x+7)2(x−2)3x(x2+7).
04:43View Solution

