Let f(x+y2)=f(x)+f(y)2forallrealxandy If f′(0) exists and equals −1andf(0)=1,thenfindf(2).Solution in Tamil
Suppose A(x,f(x))andB(y,f(y)) be any two points on the curve y=f(x).
If M is the mid-point of AB, then the coordinates of M are (x+y2,f(x)+f(y)2).
Now the foot of the perpendicular from the M on the x-axis is L. ML meets the curve y=f(x) at P.
According to the graph, the coordinates of P are (x+y2,f(x+y2))andPL>ML.
⇒ f(x+y2)>f(x)+f(y)2
But given f(x+y2)=f(x)+f(y)2, which is possible when P→M.
That is, P lies on AB. Hence y=f(x) must be a linear function.
Let f(x)=ax+b ⇒f(0)=0+b=1 (given )
and f'(x)=a ⇒f'(0)=a=−1 (given )
∴ f(x)=−x+1
∴ f(2)=−2+1=−1
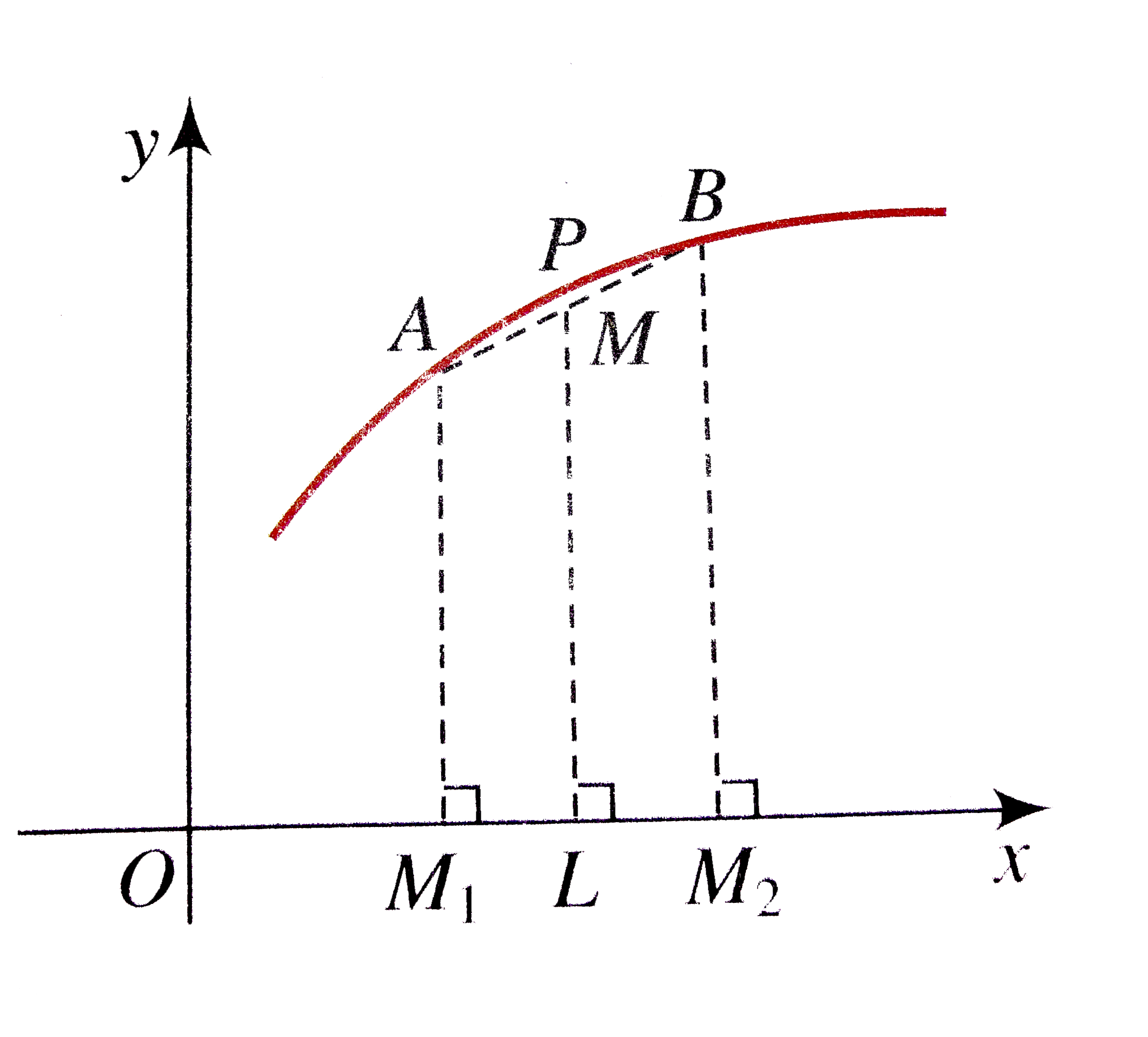
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
03:14View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=004:45View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
03:23View SolutionLet f be differentiable at x=a and let f(a)≠0. Evaluate (lim)n→∞⎧⎪ ⎪⎨⎪ ⎪⎩f(a+1n)f(a)⎫⎪ ⎪⎬⎪ ⎪⎭n.
03:17View SolutionLet f(x)=11+e1xfor x≠0 and f(0)=0 , then f(0+) does not exist b. f(0) is equal to zero c. f′(0−) is equal to 1 d. f′(0+) is equal to zero
03:11View SolutionIf f(x+y+1)={√f(x)+√f(y)}2 and f(0)=1∀x,y∈R,determ∈ef(n),n∈N.
01:42View SolutionIf f(x)=(1−x)n, then the value of f(0)+f′(0)+f''(0)2!+f'''(0)3!+......fn(0)n!.
04:32View SolutionLet f(x+y)=f(x).f(y) for all xandy. Suppose f(5)=2andf′(0)=3. Find f′(5).
04:07View SolutionIf f(x)=|x−2|andg(x)=f[f(x)],theng′(x)= ______ for x>20
04:15View SolutionA function f:R→R satisfies the equation f(x+y)=f(x)f(y) for allx,y∈Randf(x)≠0forallx∈R. If f(x) is differentiable at x=0andf′(0)=2, then prove that f′(x)=2f(x).
02:21View SolutionLet f(x+y)=f(x).f(y) for all xandy. Suppose f(5)=2andf′(0)=3. Find f′(5).
02:22View SolutionLet f(x+y)=f(x).f(y) for all xandy. Suppose f(5)=2andf′(0)=3. Find f′(5).
03:14View SolutionIf for a continuous function f,f(0)=f(1)=0,f′(1)=2andy(x)=f(ex)ef(x) , then y′(0) is equal to a. 1 b. 2 c. 0 d. none of these
05:51View Solutionlet f(x)=ex,g(x)=sin−1xand h(x)=f(g(x)) t h e n f i n d h′(x)h(x)
06:08View SolutionIf f(x)=limn→∞n(x1n−1),thenforx>0,y>0,f(xy) is equal to : (a)f(x)f(y) (b) f(x)+f(y) (c)f(x)−f(y) (d) none of these
01:38View SolutionIf f(x)=(1+x)n, then the value of f(0)+f′(0)+f''(0)2!+f'''(0)3!+......fn(0)n!.
04:27View Solution

