Find the value of a for which ax2+(a−3)x+1<0 for at least one positive real x .Solution in Tamil
Let f(x)=ax2+(a−3)x+1
Case (i)
If a>0, then f(x) will be negative only for those values of x which lie between the roots.
Since f(0)=1>0, the favourable graph according to the questions is shown in the following figure.
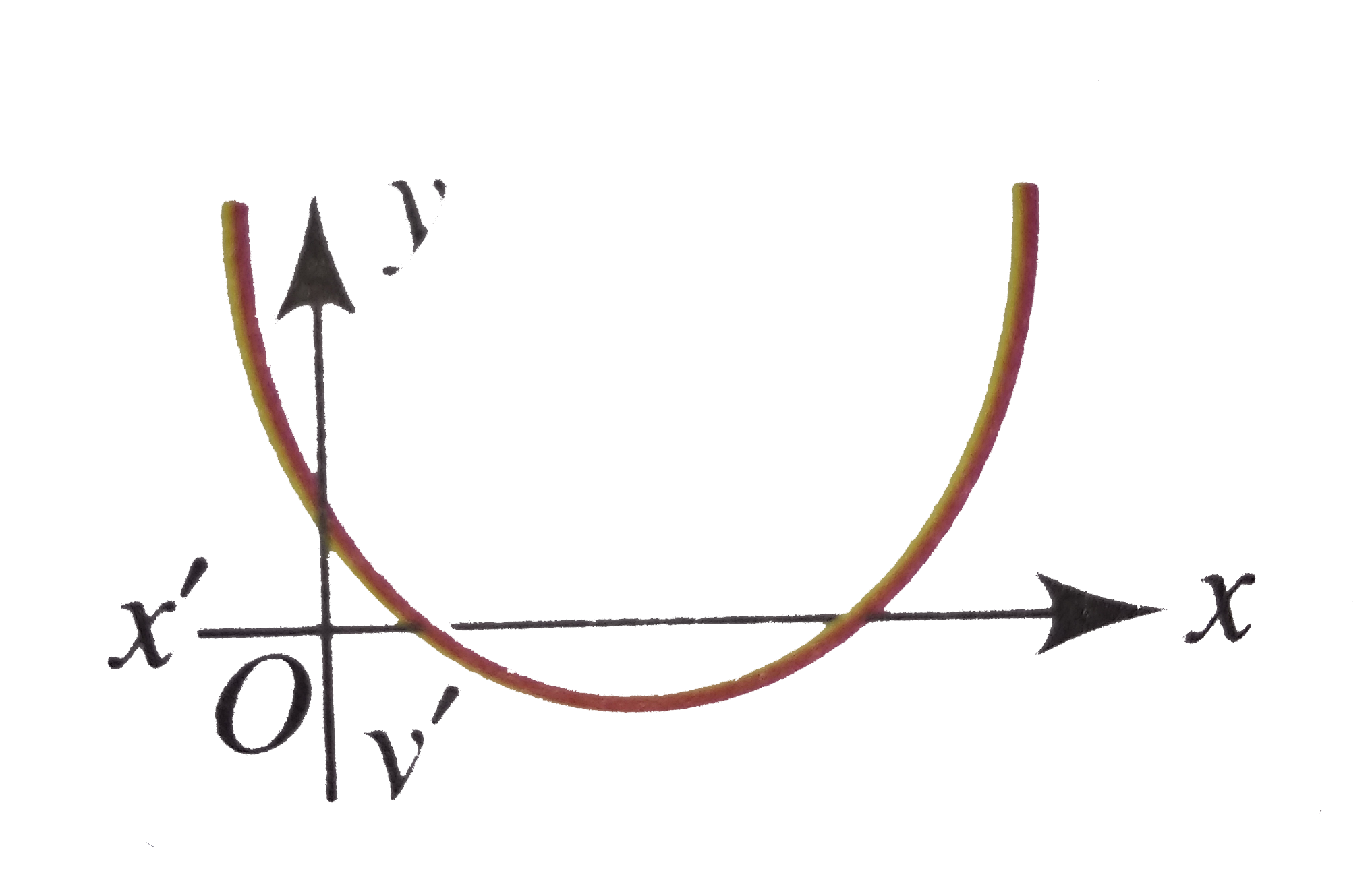
From the graph, we can see that both the roots are positive.
For this
(i) D>0⇒(a−3)2−4a>0
⇒a<1ora>9 (i)
(ii) Sum >0 and product >0
⇒−(a−3)>0and1/a>0
⇒a<3 (ii)
From (i) and (ii), a<1
But a>0⇒a∈(0,1)
Case (ii) : a<0
Since f(0)=1>0, the graph is as shown in the following figure :
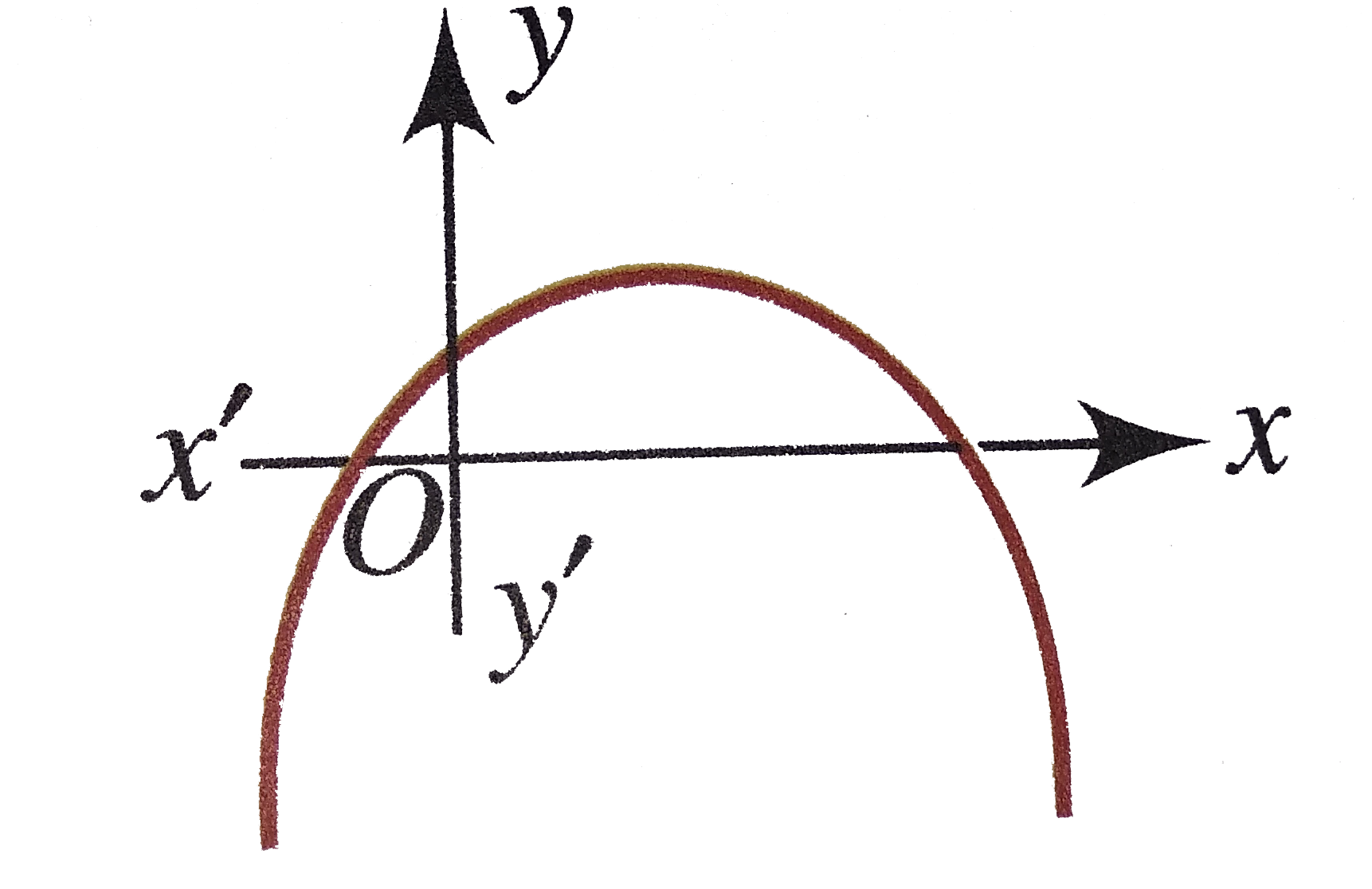
From the graph ax2+a(a−3)x+1<0, for at least one positive x.
Case (iii): a=0
If a=0,f(x)=−3x+1
⇒ f(x)<0,∀x>1/3
Thus, from all the cases, the required set of values of 'a' is (−∞,1).
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionFind the least positive value of k for which the equation x2+kx+4=0 has real roots.
View SolutionThe set of values of 'a' for which the inequality x^(2)-(a+2)x-(a+3)<0 is satisfied by atleast one positive real x,
View SolutionFind all real value of a for which the equation x^(4)+(a-1)x^(3)+x^(2)+(a-1)x+1=0 possesses at least two distinct positive roots
View SolutionFind the values of the parameter a for which 4^(x)-a.2^(x)-a+3<=0 for atleast one real x.
View SolutionIf the inequality x^(2)+kx+k<0 is satisfied for at least one real x ,then find the smallest positive interaer value of k.
View Solutionk का वह निम्नतम धनात्मक मान ज्ञात करो जिसके लिए समीकरण x2+kx+4=0 के मूल वास्तविक हों।
View SolutionFind the value of a for which ax2+(a−3)x+1<0 for at least one positive real x.
View SolutionFind all real value of a for which the equation x4+(a−1)x3+x2+(a−1)x+1=0 possesses at least two distinct positive roots
View SolutionFind the least positive value of k for which the equation x2+kx+4=0 has real roots.
View SolutionFind the values of k so that the quadratic equation x2 + 2(k-1)x + k+5 = 0 has atleast one positive root.
View SolutionFor real x,the least value of (x-2)(x-3)+1 is___
View SolutionFind all the values of the parameter 'a' for which the inequality 4x−a2x−a+3≤0 is satisfied by at least one real x.
View SolutionIfx2−(a−3)x+a=0 has at least one positive root,then
View Solution
