Solve x2−4−[x]=0 (where [] denotes the greatest integer function).Solution in Tamil
The best method to solve such an equation is graphical one.
Give equation is x2−4=[x].
Then the solutions to the question are values of x where the graphs of y=x2−4andy=[x] interesect.
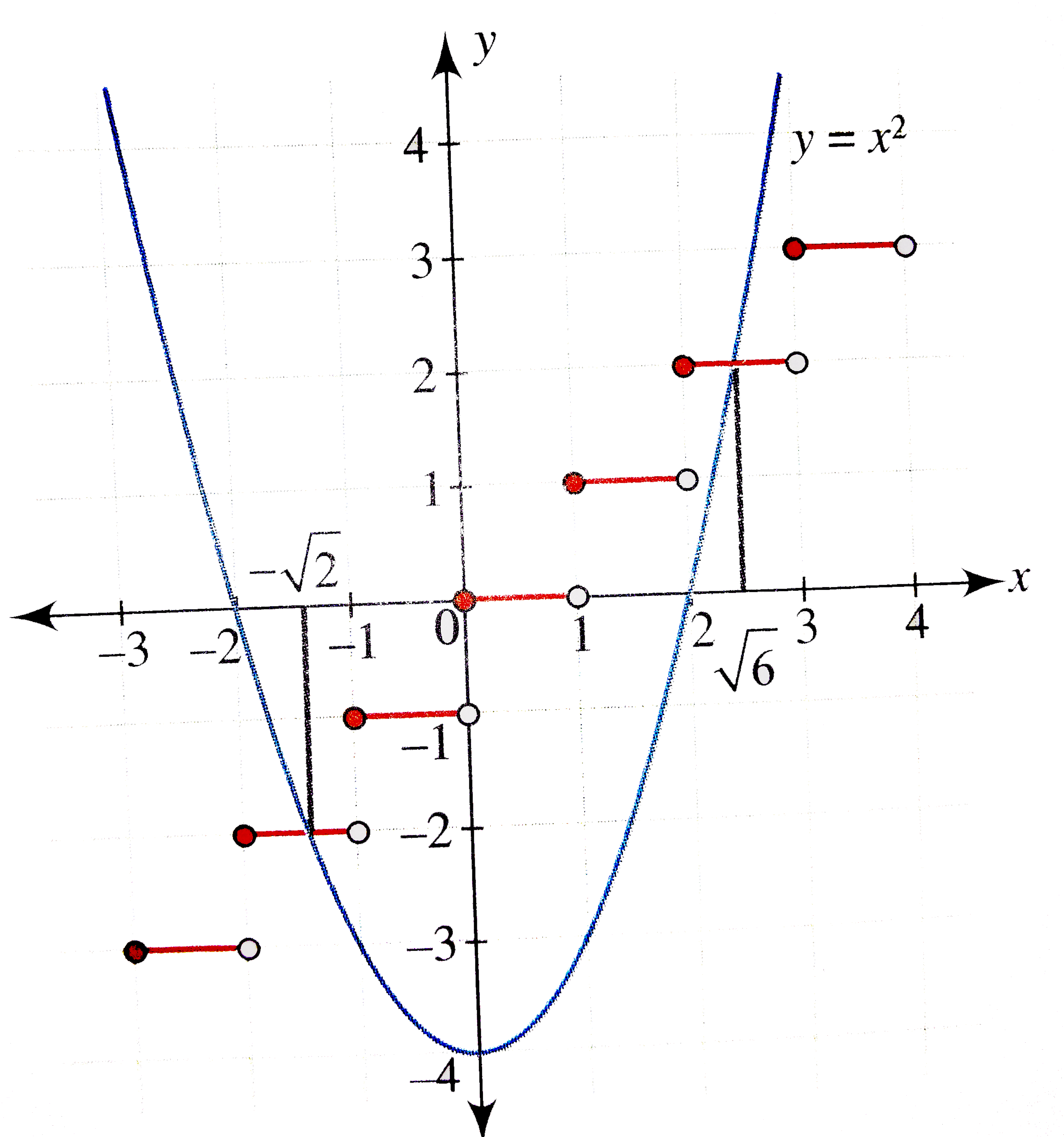
From the figure, it is seen that the graphs intersect when
x2−4=2andx2−4=2.
⇒ x2=6orx2k=2
⇒ x=x=√6or−√2
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
05:20View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=004:32View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
04:30View SolutionSolve x2−4−[x]=0 (where [] denotes the greatest integer function).
03:48View SolutionIf [log_(2)((x)/([x]))]>=0, where [.] denote the greatest integer function,then
04:42View SolutionSolve : 4{x}=x+[x](where [⋅] denotes the greatest integer function and {⋅} denotes the fractional part function.
02:28View SolutionSolve x^2-4-[x]=0 (where [] denotes the greatest integer function).
03:30View SolutionSolve x^2-4x-[x]=0 (where [] denotes the greatest integer function).
02:02View SolutionSolve : 4{x}=x+[x](where [⋅] denotes the greatest integer function and {⋅} denotes the fractional part function.
01:51View SolutionSolve x^2-4-[x]=0 (where [] denotes the greatest integer function).
01:28View SolutionSolve
limx→0+[sinxx]
(where [.] denotes greatest integer function.)01:41View SolutionSolve
limx→0−[sinxx]
(where [.] denotes greatest integer function.)04:48View SolutionSolve
limx→0+[tanxx]
(where [.] denotes greatest integer function.)02:00View SolutionSolve
limx→0−[tanxx]
(where [.] denotes greatest integer function.)05:13View SolutionSolve x^2-4-[x]=0 (where [] denotes the greatest integer function).
06:11View SolutionSolve : 4{x}= x+ [x] (where [*] denotes the greatest integer function and {*} denotes the fractional part function.
03:39View Solution

