Let f:R→R be a function defined by f(x)=max.{x,x3}. The set of all points where f(x) is NOT differenctiable is
(a) {−1,1}
(b) {−1,0}
(c ) {0,1}
(d) {−1,0,1} Solution in Tamil
We have f(x)=max.{x,x3}
Draw the graphs of y=xandy=x3
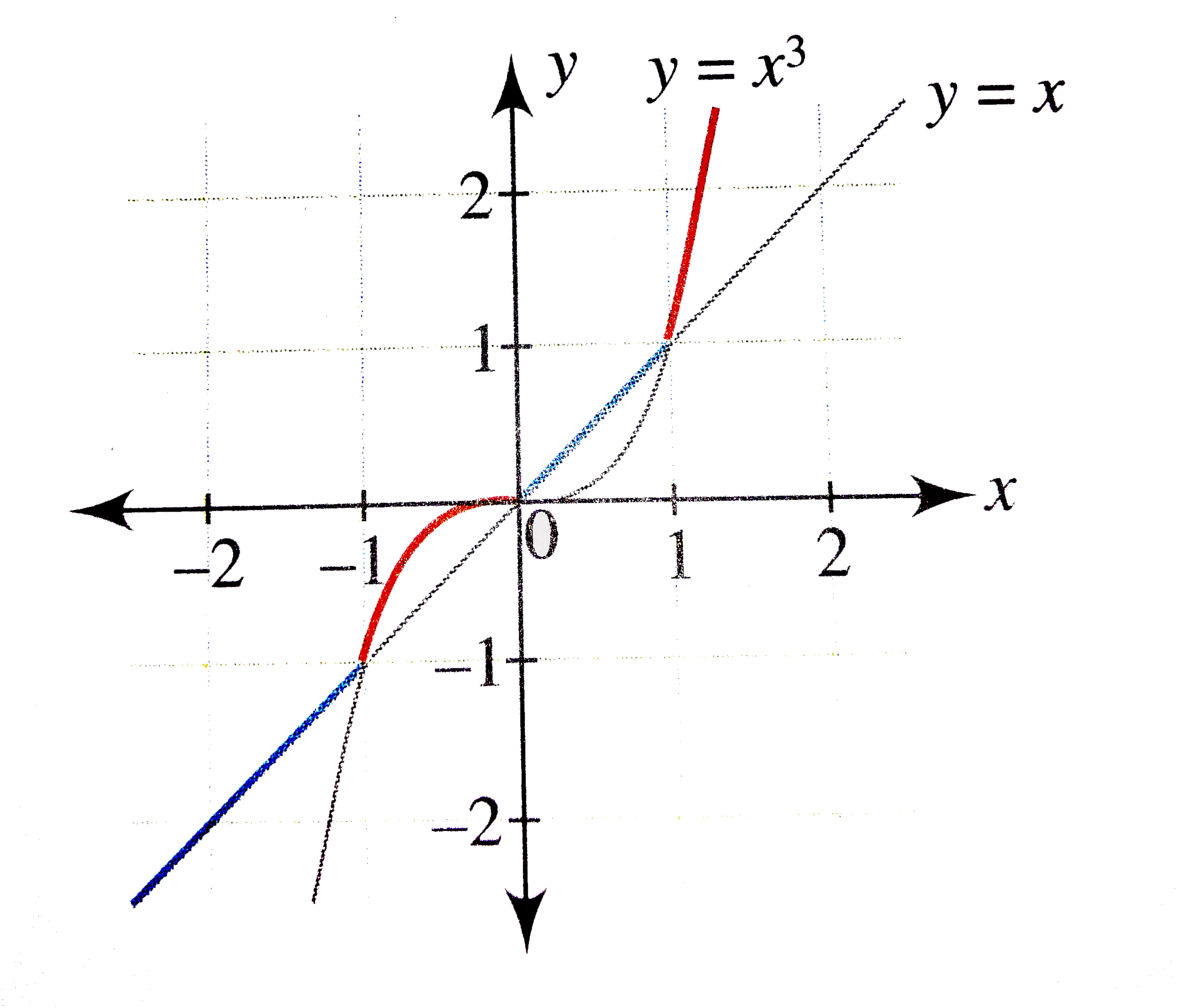
Graph of y=f(x) is combination of the combination of the blue and red-lined graphs.
From the graph, y=f(x) is non-differentiable at x=−1,x=0andx=1.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
07:18View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=009:29View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
06:40View SolutionLet f(x)=max{1+sinx,1,1−cosx},x∈[0,2π],andg(x)=max{1,|x−1|},x∈R. Then (a)g(f(0))=1 (b) g(f(1))=1 (c)f(f(1))=1 (d) f(g(0))=1sin1
02:03View SolutionLet f[0,1]→R (the set of all real numbers be a function.Suppose the function f is twice differentiable, f(0)=f(1)=0,and satisfies f'(x)–2f'(x)+f(x)≤ex,x∈[0,1].Which of the following is true for 0<x<1?
04:51View SolutionLet f(x)=x−[x],x∈R, then f′(12) is a. 32 b. 1 c. 0 d. -1
01:39View SolutionLet f:R→R+ be defined by f(x)=ax, a>0 and a≠1 . Write f−1(x) .
04:52View SolutionLet R be the set of all real numbers and let f be a function from R to R such that
f(X)+(X+12)f(l−X)=1,
for all ξnR. Then 2f(0)+3f(1) is equal to-02:47View SolutionIf f:R−{0}→R is defined by f(x)=x3−1x3, then S.T f(x)+f(1/x)=0.
07:18View SolutionLet f:(0,∞)→R be a differentiable function such that f'(x)=2−f(x)x for all x∈(0,∞) and f(1)=1, then
04:02View SolutionLet f:R→R+ be defined by f(x)=ax, a>0 and a≠1 . Write f−1(x) .
03:36View SolutionLet f be a twice differentiable function defined on R such that f(0) = 1, f'(0) = 2 and f'(x)≠0 for all x∈R. If ∣∣∣f(x) f'(x)f'(x) f''(x)∣∣∣=0, for all x∈R, then the value of f(1) lies in the interval:
01:39View SolutionLet R be the set of all real numbers and f:[1,−1]→R be
defined by f(x)={xsin(1x)x≠00x=002:07View SolutionLet f:R→R be a function defined by f(x)=max{x,x3}. The set of all points where f(x) is not differentiable is
05:27View SolutionIf f:R−{0}→R is defined by f(x)=x3−1x3, then S.T f(x)+f(1/x)=0.
02:02View SolutionLet f:R→R be a function defined by f(x)=∣x] for all x∈R and let A=[0,1), then f−1(A) equals
06:15View Solution

