Find the equivalent definition of f(x)=max.x2,(−x)2,2x(1−x)whre0≤x≤1Solution in Tamil
Let us consider f1(x)=x2,f2(x)=(1−x)2andf3(x)=2x(1−x)
Now taking graph for f1(x),f2(x)andf3(x),
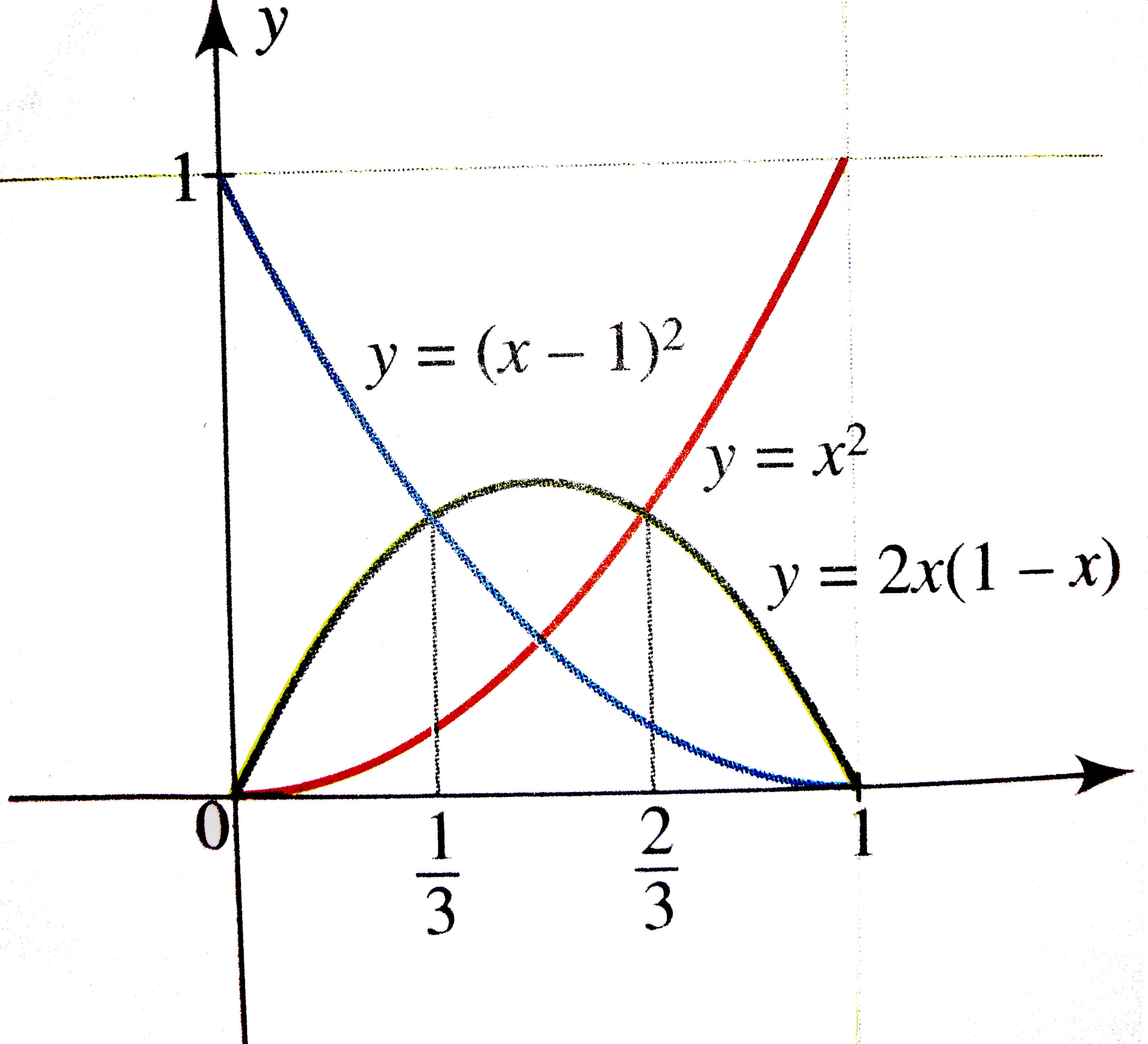
Since we want to find the maximum of three function f1(x),f2(x)andf3(x) :
f(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩(1−x)2,0≤x<132x(1−x),13≤x<23,x2,23≤x≤1
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
06:11View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=002:09View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
07:44View SolutionEvaluate: (i)∫1−1f(x)dx,where,f(x)={1−2x,x≤0;1+2x,x≥0}, (ii) ∫4−1f(x)dx,where,f(x)={2x+8,−1≤x≤2;6x,2≤x≤4}
05:10View SolutionLet f(x)=x−[x], for ever real number x,where[x] is the greatest integer less than or equal to x. Then, evaluate ∫1−1f(x)dx .
05:20View SolutionFind the equivalent definition of f(x)=max{x2,(1−x)2,2x(1−x)}where 0≤x≤1
10:46View SolutionFind (lim)x→1f(x) ,where f(x)={x2−1x≤1−x2−1x>1
06:58View SolutionDiscuss the applicability of Rolles theorem on the function f(x)={x2+1, when 0≤x≤13−x, when 1<x≤2
03:16View SolutionSolve for xandy:√3sinx+cosx=8y−y2−18,where0≤x≤4π,y∈R
04:54View SolutionFind the equivalent definition of f(x)=max{x2,(1−x)2,2x(1−x)}where 0≤x≤1
03:01View SolutionDiscuss monotonocity of f(x)=xsinxand g(x)=xtanx,where<x≤1
01:58View SolutionDraw the graph of the function f(x)=max.sinx,cos2x,x∈[0,2π]. Write the equivalent definition of f(x) and find the range of the function.
02:00View SolutionFind the equivalent definition of f(x)=max.x2,(−x)2,2x(1−x)where0≤x≤1
04:17View SolutionLet f(x)=x−[x], for ever real number x,where[x] is the greatest integer less than or equal to x. Then, evaluate ∫1−1f(x)dx .
03:42View SolutionFind (lim)x→1f(x),wheref(x)=[x2−1,x≤1−x2−1,x>1
06:31View SolutionEvaluate the following integral: ∫90f(x)dx, where f(x)=sinx, 0≤x≤π/2<br>
where f(x)=1,π2≤x≤3
where f(x)=ex−3, 3≤x≤907:11View Solution

