The coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0), respectively. The equation of the diagonal CE is Solution in Tamil
√3x+y=4
x+√3y+4=0
x+√3y=4
none of these
The correct Answer is:C
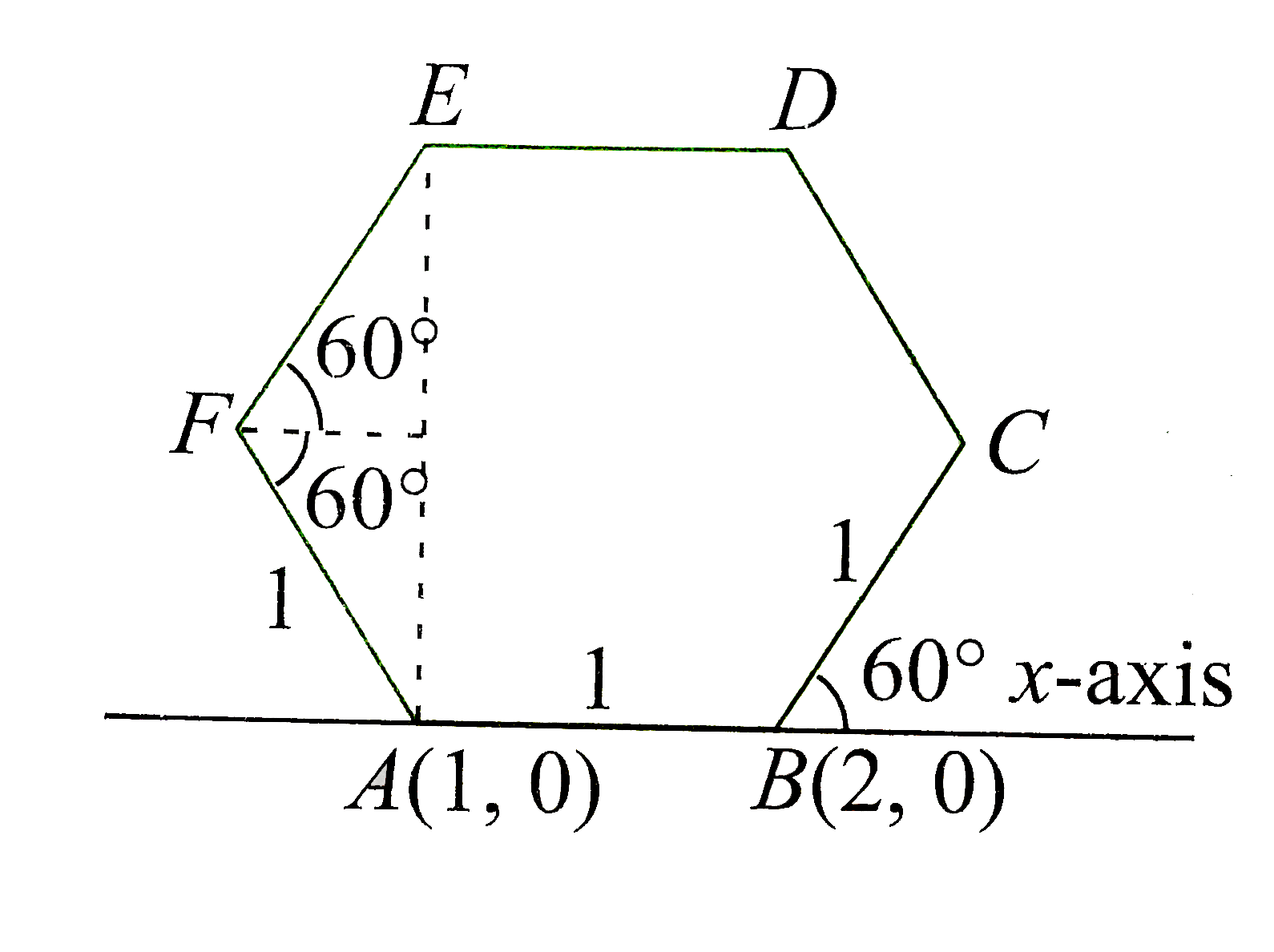
AB=1
or C≡(2+1×cos60∘,1×sin60∘)≡(52,√32)
E≡(1,1×sin60∘+1×sin60∘)≡(1,√3)
Therefore, the equation of CE is
y−√3=−1√3(x−1)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)30videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)27videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.65videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
05:07View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is11:59View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
06:14View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
02:10View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
03:25View SolutionThe coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0) respectively.The equation of the diagonal CE is:
05:38View SolutionThe coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0), respectively. The equation of the diagonal CE is (a)√3x+y=4 (b) x+√3y+4=0 (c)x+√3y=4 (d) none of these
View SolutionLet ABCDEF be a regular hexagon whose centre is at the origin.(A,B,C,D,E and F are in anticlockwise direction).If the coordinates of A be 1+i then c lies in
05:54View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
07:04View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
05:44View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
 02:19View Solution
02:19View SolutionA, B, C, D, E, F in that order, are the vertices of a regular hexagon with centre orgin. If the position vectors of the vertices A and B are respectively, 4ˆi+3ˆj−ˆkand−3ˆi+ˆj+ˆk, then DE is equal to
04:50View SolutionA,B, and C are vertice of ΔABC,D,EandF are mid point of side AB,BC and AC respectively. If the coordinates of A, D and F are (-3,5),(5,1) and (-5,-1) respectively. Find the coordinates of B,C and E.
02:06View SolutionThe coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0), respectively. The equation of the diagonal CE is (a)√3x+y=4 (b) x+√3y+4=0 (c)x+√3y=4 (d) none of these
04:58View SolutionThe coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0) respectively. The equation of the diagonal CE is:
02:52View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=34 , then write Area (ABC):Area(DEF) .
06:44View Solution

