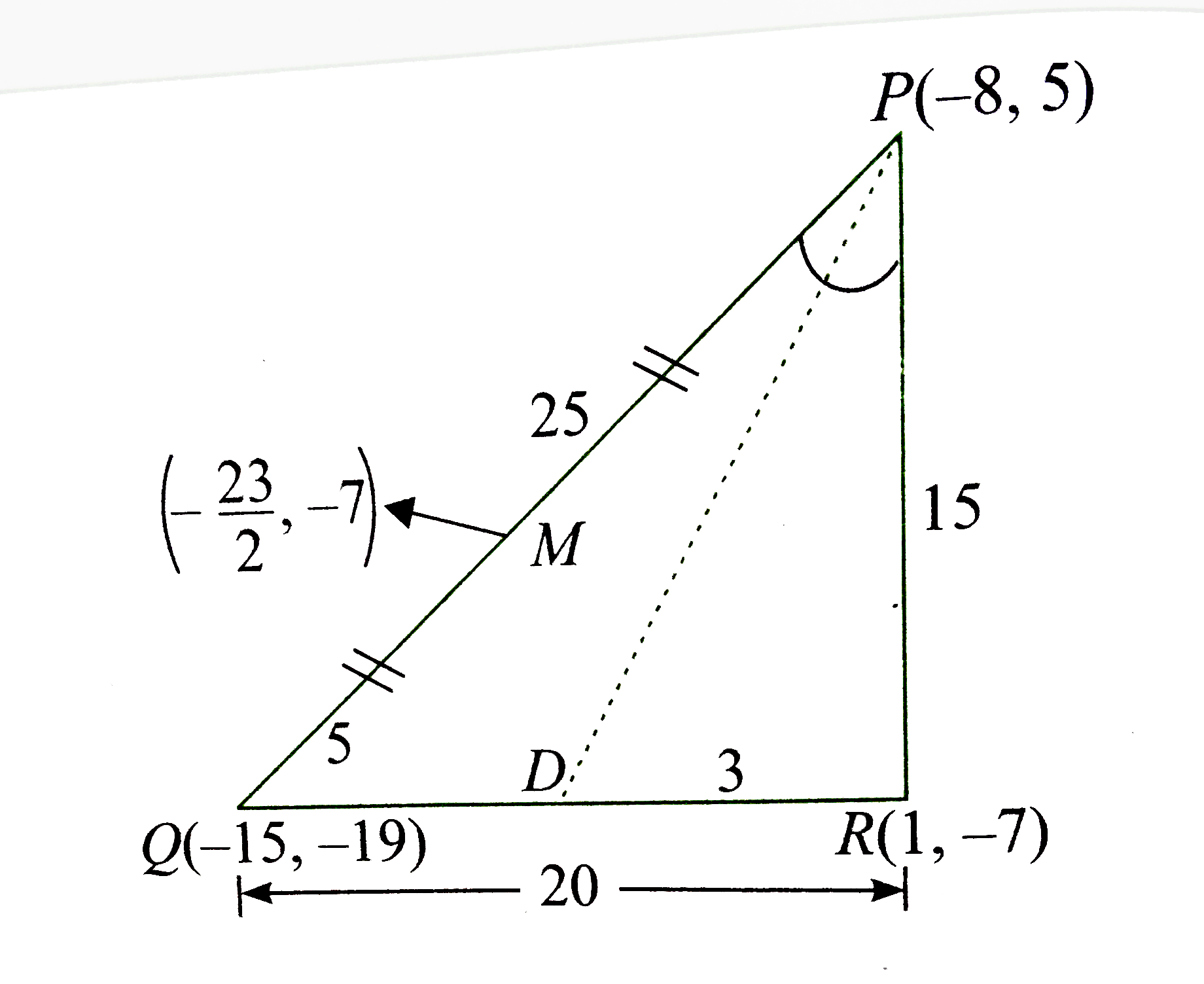
Consider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The distance between the orthocenter and the circumcenter of triangle PQR is Solution in Tamil
The correct Answer is:A
Since the triangle is right-angled, the circumcenter is the midpoint of PQ and the orthocenter is R(1, -7). Hence,
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)
8 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)
13 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View Solutionstraight line L with negative slope passes through the point (9,4) cuts the positive coordinate axes at the point P and W As L. Varies, find the minimum value of |OP|+|OQ| , where O is origin .
View SolutionIf P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionThe interior angle bisector of angle P for the trangle PQR whose coordinates of the veetices are P(−8,5);Q(−15,−19)andR(1,−7) has the equation ax+2y+c=0, then (a,c)= a=11 a=10 c=78 c=80
View SolutionThe interior angle bisector of angle A for the triangle ABC whose coordinates of the vertices are A(−8,5),B(−15,−19)andC(1,−7) has the equation ax+2y+c=0 Find 'a' and 'c'
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The distance between the orthocenter and the circumcenter of triangle PQR is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(−8,5),Q(−15,−19), and R(1,−7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The radius of the in circle of triangle PQR is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The radius of the in circle of triangle PQR is
The sum a + c is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The distance between the orthocenter and the circumcenter of triangle PQR is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The radius of the in circle of triangle PQR is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The radius of the in circle of triangle PQR is
The sum a + c is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15,-19), and R(1,-7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0
The distance between the orthocenter and the circumcenter of triangle PQR is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15,-19), and R(1,-7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0
The radius of the incircle of triangle PQR is
View Solution
