Let ABCD be a parallelogram the equation of whose diagonals are AC:x+2y=3; BD: 2x + y = 3. If length of diagonalAC=4 units and area of ABCD=8 sq. units. (i) The length of the other diagonal is (ii) the length of side AB is equal toSolution in Tamil
10/3
2
20/3
none of these
The correct Answer is:C
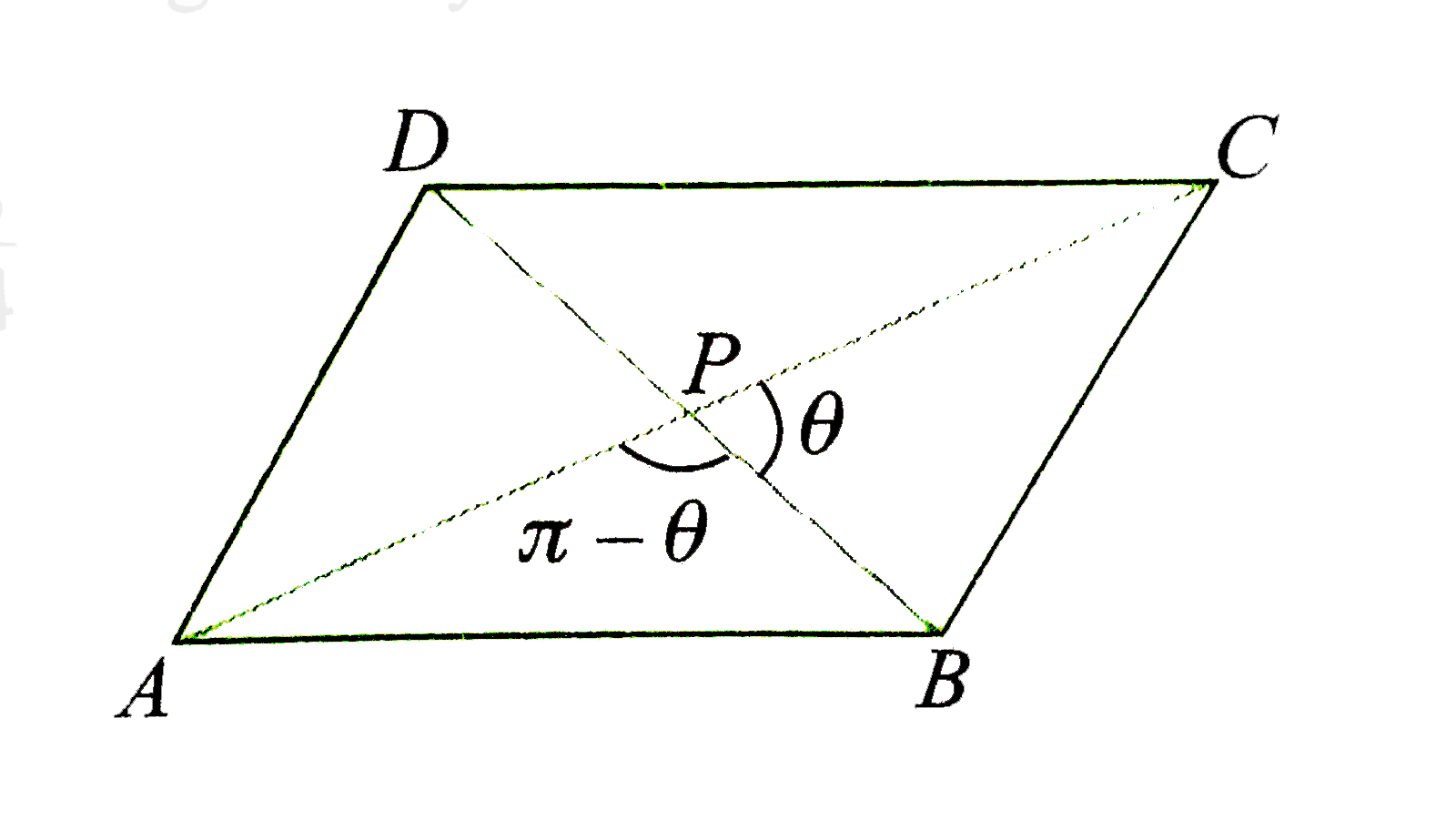
Angle between the diagonal is given by
tan θ=∣∣
∣∣−12+21+1∣∣
∣∣=34
or sinθ=35
Area of ΔCPB is
12×PC×PBsinθ=2
or PB=103
or BD=203
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)
8 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)
13 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View Solutionstraight line L with negative slope passes through the point (9,4) cuts the positive coordinate axes at the point P and W As L. Varies, find the minimum value of |OP|+|OQ| , where O is origin .
View SolutionIf P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionLet ABCD be a parallelogram the equation of whose diagonals are AC : x+2y =3; BD: 2x + y = 3. If length of diagonal AC =4 units and area of ABCD = 8 sq. units. (i) The length of the other diagonal is (ii) the length of side AB is equal to
View SolutionABCD is a rhombus whose diagonals intersect at O. If AB=10cm, diagonals BD=16 cm , find the length of diagonal AC
View Solution3x−2y+1=0and2x−y=0 are the equation of the sides ABandAD of the parallelogram ABCD and the equation of a diagonal of the parallelogram is 5x−3y−1=0. The area of the parallelogram ABCD is : (A) 2 sq. units (B) 4 sq. units (C) 6 sq. units (D) 8 sq. units
View SolutionDiagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA= 3 cm and OD = 2 cm, determine the lengths of AC and BD.
View SolutionLet ABCD be a parallelogram whose equations for the diagonals AC and BD are x+2y=3 and 2x+y=3, respectively.
The length of side AB is equal to
View SolutionIn a parallelogram ABCD,AB=ˆi+ˆj+ˆkand diagonal AC=ˆi−ˆj+ˆk and area of parallelogram is √8sq units, ∠BAC is equal to
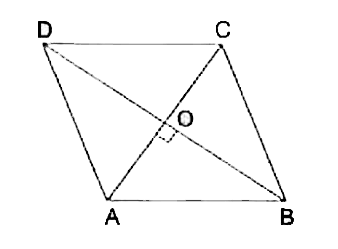
View SolutionIn the adjacent figure , ABCD is a rhombus whose diagonals AC and BD intersect at a point O. If side AB=10 cm and diagonal BD=16 cm , find the length of diagonal AC.
View SolutionABCD is a parallelogram, with AC, BD as diagonals, then −AC−−BD is equal to
View SolutionDiagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA= 3 cm and OD = 2 cm, determine the lengths of AC and BD.
View SolutionLet ABCD be a parallelogram the equation of whose diagonals are AC:x+2y=3; BD: 2x + y = 3. If length of diagonalAC=4 units and area of ABCD=8 sq. units. Find the length of the other diagonal is a. 10/3 b. 2 c. 20/3 d. None of these
View Solution
