Let C be a curve passing through M(2,2) such that the slope of the tangent at any point to the curve is reciprocal of the ordinate of the point. If the area bounded by curve C and line x=2 is A, then the value of 3A2 is__.Solution in Tamil
The correct Answer is:8
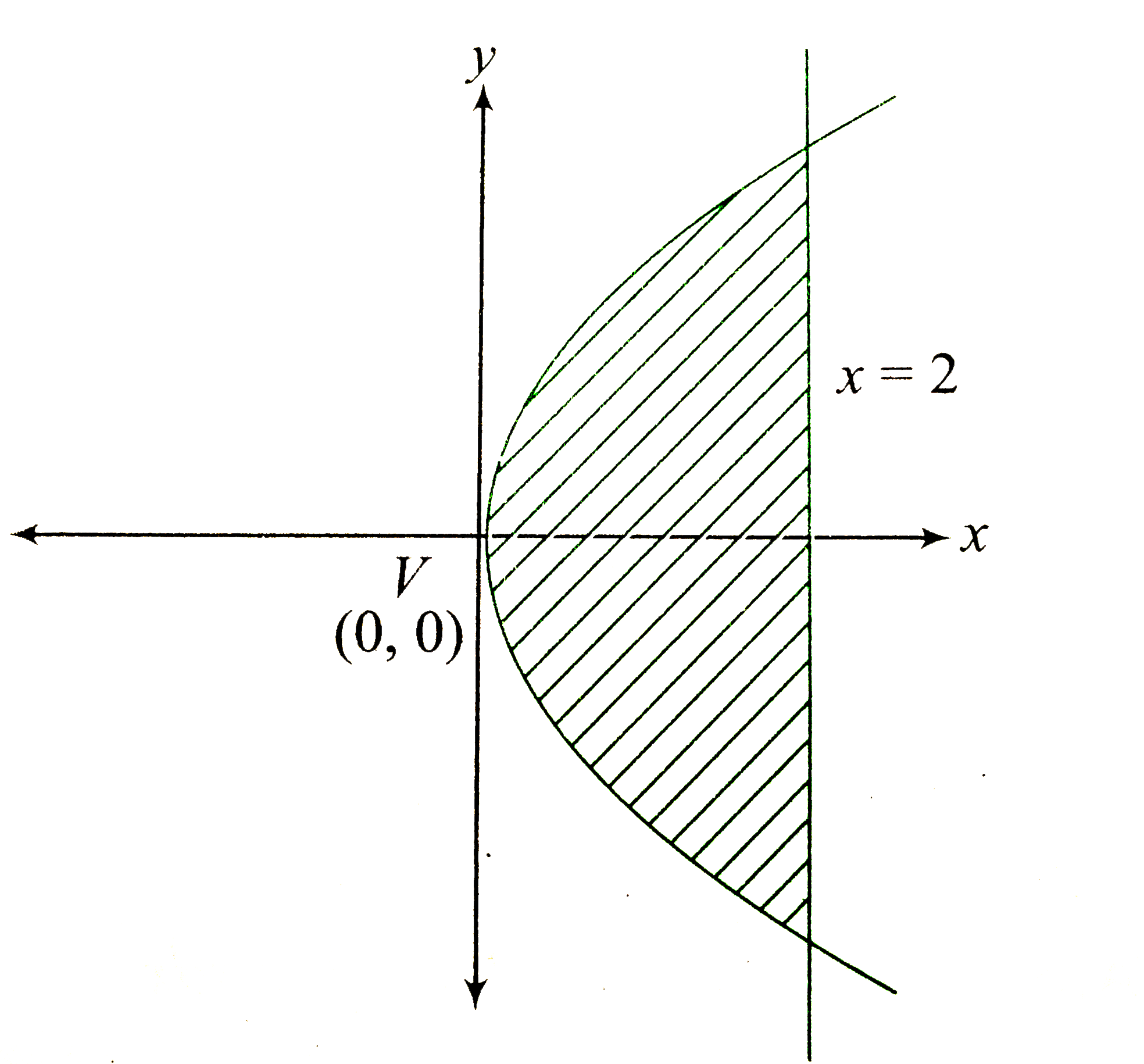
Let P(x,y) be any point on the curve C.
Now, dydx=1y
or ydy=dx⇒y22=x+k
Since the curve passes through M(2,2), so k=0
⇒ y2=2x
∴ Required area =22∫0√2xdx=2√2×23(x3/2)20
=43√2×2√2=163 sq. unit
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year10videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year9videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)4videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
The area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
01:59View SolutionFind the area bounded by the curves x+2|y|=1 and x=0.
01:38View SolutionMatch the following lists :
 03:38View Solution
03:38View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
04:02View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
02:53View SolutionObtain the equation of the curve passing through the point (4,3) and at any point the gradient of the tangent to the curve is the reciprocal of the ordinate of the point.
02:09View SolutionThe slope of a curve at any point is the reciprocal of twice the ordinate at that point and it passes through the point (4,3). The equation of the curve is:
View SolutionLet C be a curve passing through M(2,2) such that the slope of the tangent at anypoint to the curve is reciprocal of the ordinate of the point. If the area bounded by curve C and lin x=2i s A ,t h e nt h e v a l u e of 3A2i s__
01:09View SolutionLet C be a curve passing through M(2,2) such that the slope of the tangent at any point to the curve is reciprocal of the ordinate of the point. If the area bounded by curve C and line x=2 is A, then the value of 3A2 is__.
04:25View SolutionA curve is passing through the point (4,3) and at any point the gradient of the tangent to the curve is reciprocal of the ordinate of the point. Obtain the equation of the curve.
02:49View SolutionThe slope of the tangent to the curve at any point is the reciprocal of four times the ordinate at that point. The curve passes through (2, 5). Find the equation of the curve.
01:37View SolutionThe slope of a curve at any point on it is the reciprocal of twice the ordinate at that point. If the curve passes through (4,3) then its equation is
02:24View SolutionThe slope of a curve at any point on it is the reciprocal of twice of ordinate at that point. If the curve passes through (4,3) then the equation is
02:08View SolutionLet C be a curve passing through M(2,2) such that the slope of the tangent at anypoint to the curve is reciprocal of the ordinate of the point. If the area bounded by curve C and line x=2 is A ,then the value of 3A2i s__
05:09View SolutionLet C be a curve passing through M(2,2) such that the slope of the tangent at any point to the curve is reciprocal of the ordinate of the point. If the area bounded by curve C and line x=2 is A, then the value of 3A2 is__.
01:49View Solution

