Question

Consider the two curves $C_1:y=1+\cos x\text{and}{C}_2:y=1+\cos (x-\alpha )\text{for}\alpha \in (0,\frac{\pi }{2}),\text{where}x\in [0,\pi ].$ Also the area of the figure bounded by the curves $C_1,C_2,\text{and}x=0$ is same as that of the figure bounded by $C_2,y=1,\text{and}x=\pi$.
For the values of $\alpha$, the area bounded by $C_1,C_2,x=0\text{and}x=\pi$ is

Answer

1

Explanation

`"Given that "D_(1)=D_(2)`
`overset(c)underset(1)int((1)/(x)-log x)dx=overset(a)underset(c)int(logx-(1)/(x))dx`
`((-1)/(x^(2))-x(logx-1))_(1)^(c)=(x(logx-1)+(1)/(x^(2)))_(c)^(a)`

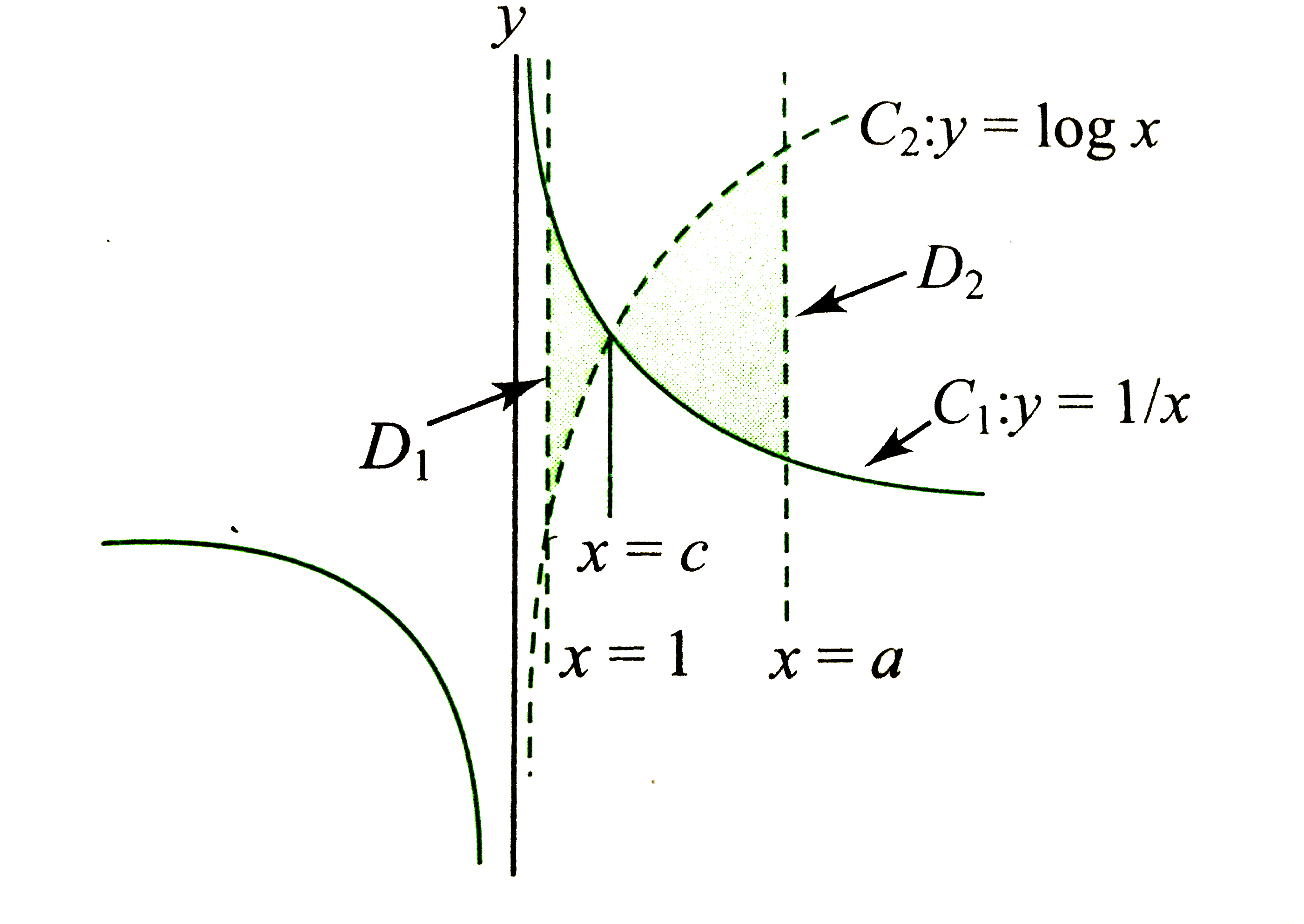
`therefore" "0=a(log a-1)+(1)/(a^(2))`
`therefore" "a=1`