If S is the sum of cubes of possible value of c for which the area of the figure bounded by the curve y=8x2−x5, then straight lines x=1andx=c and the abscissa axis is equal to 163, then the value of [S],where[.] denotest the greatest integer function, is____Solution in Tamil
The correct Answer is:2
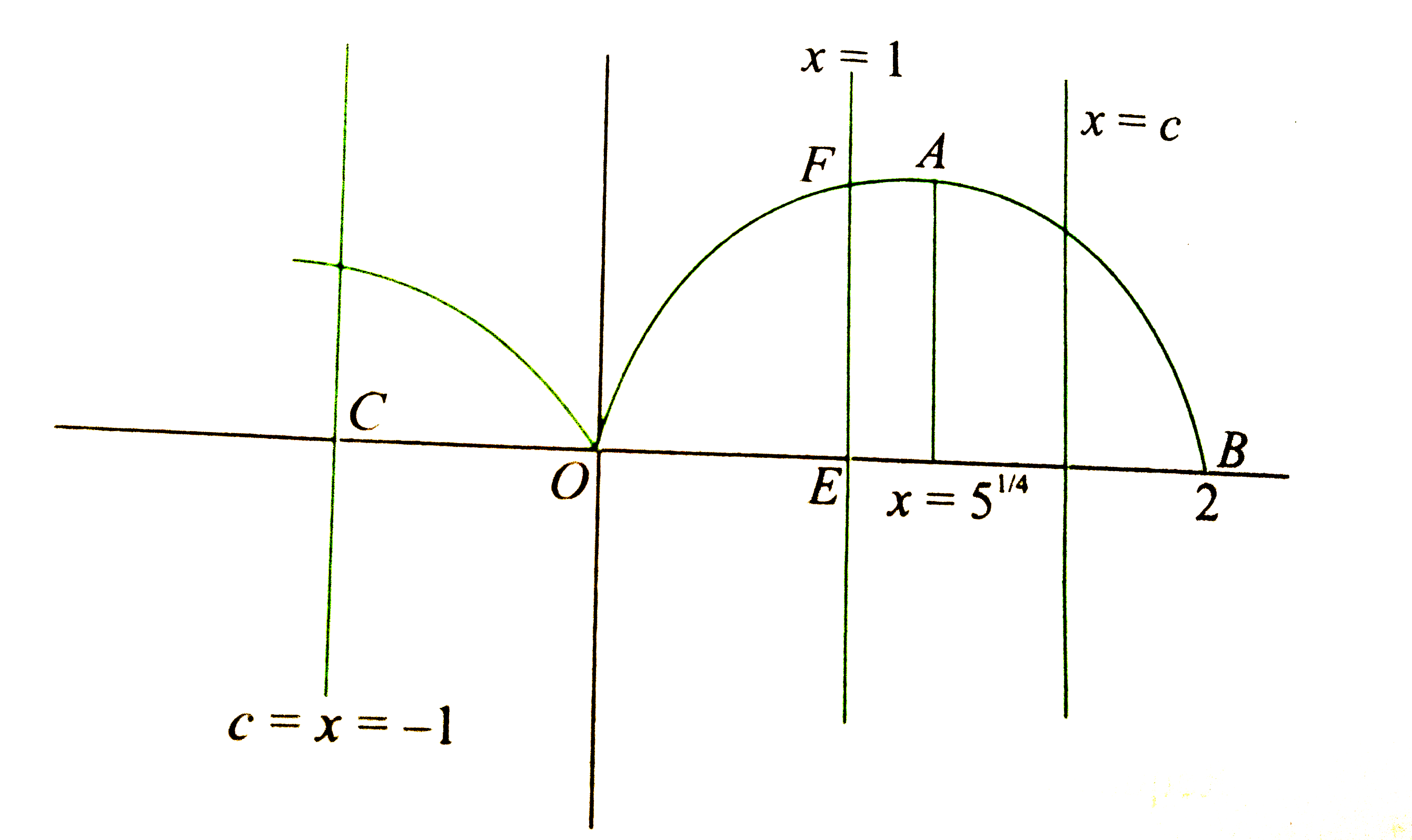
Given that c∫1ydx=163
⇒ c∫1(8x2−x5)dx=163c=(8−√17)1/3 (c>0)
Area OFE=c∫0(8x2−x5)dx=83 (C>0)
so c=−1
Hence, c=−1and(8−√17)1/3
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year10videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year9videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)4videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
The area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
05:54View SolutionFind the area bounded by the curves x+2|y|=1 and x=0.
04:02View SolutionMatch the following lists :
 03:19View Solution
03:19View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
07:43View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
10:32View SolutionIf S is the sum of possible values of c for which the area of the figure bounded by the curves y=s∈2x, the straight lines x=π6,x=c, and the abscissa axis is equal to 12, then the value of π/S is____
06:05View SolutionIf S is the sum of cubes of possible value of c for which the area of the figure bounded by the curve y=8x2−x5, then straight lines x=1andx=c and the abscissa axis is equal to 163, then the value of [S],where[.] denotest the greatest integer function, is____
04:45View SolutionWhich of the following is the possible value/values of c for which the area of the figure bounded by the curves y=sin2x, the straight lines x=π/6,x=c and the abscissa axis is equal to 1/2?
03:25View SolutionFind the value of ‘c’ for which the area of the figure bounded by the curve, y=8x2–x5, the straight lines x = 1 and x = c and the abscissa axis is equal to 16/3.
01:35View SolutionColumn I, Column II Area enclosed , q. 1. sq. units The smaller area included between the curves √x+√|y|=1 and |x|+|y|=1 , r. 4 sq. units Area bounded by the curves y=[x264+2](where[.]de¬es the greatest integer function), y=x−1andx=0 above the x-axis., s. 2/3 sq. units
01:54View SolutionWhich of the following abnormalities is due to X-linked recessive mutation ?
01:58View SolutionIf S is the sum of cubes of possible value of c for which the area of the figure bounded by the curve y=8x2−x5, then straight lines x=1andx=c and the abscissa axis is equal to 163, then the value of [S],where[.] denotest the greatest integer function, is____
02:27View SolutionThe integral ∫1.50[x2]dx,where[.] denotoes the greatest integer function, equals ...........
04:58View SolutionEvaluate: ∫1000(x−[x]dx(where[.] represents the greatest integer function).
05:18View SolutionWhich of the following is the possible value/values of c for which the area of the figure bounded by the curves y=sin2x, the straight lines x=π/6,x=c and the abscissa axis is equal to 1/2?
13:14View Solution

