Let f:[0,∞)→R be a continuous function such that f(x)=1−2x+∫x0ex−tf(t)dt for all x∈[0,∞). Then, which of the following statements(s) is (are)) TRUE?Solution in Tamil
a)The curve y=f(x) passes through the point (1,2)
b)The curve y=f(x) passes through the point (2,-1)
c)The area of the region {(x,y)∈[0,1]×R:f(x)≤y≤√1−x2} is π−24
d)The area of the region {(x,y)∈[0,1]×R:f(x)≤y≤√1−x2} is π−14
The correct Answer is:B, C
f(x)=1−2x+x∫0ex−1f(t)dt
⇒ f(x)=1−2x+exx∫0e−tf(t)dt ...(i)
Differentiating w.r.t. x, we get
f'(x)=−2+exe−xf(x)+exx∫0e−tf(t)dt ...(ii)
Subtracting (i) from (ii), we get
f'(x)−f(x)=−2+f(x)−1+2x
⇒ f'(x)−2f(x)=2x−3
This is linear differential equation.
I.F.=e∫−2dx=e−2x
Therefore, solution is
y⋅e−2x=∫(2x−3)e−2xdx+c
⇒ y⋅e−2x=(2x−3)⋅e−2x−2−∫2×e−2x−2dx+c
⇒ y⋅e−2x=−(2x−3)e−2x2−e−2x2+c
⇒ y⋅e−2x=(1−x)e−2x+c
⇒ y=(1−x)+c.e2x ...(iii)
Putting x=0 in (i), we get f(0)=1.
So, from above equation, we have
1=1+c⇒c=0
Now, (iii) reduces to y=1-x, which passes through point (2,-1).
Now,f(x)≤y≤√1−x2
⇒ 1−x≤y≤√1−x2
1−x≤y represents the region above the line 1−x=yandy≤√1−x2 represents the region inside the semicircle (lying above x-axis) x2+y2=1.
So, common region is as the shaded one in the following figure :
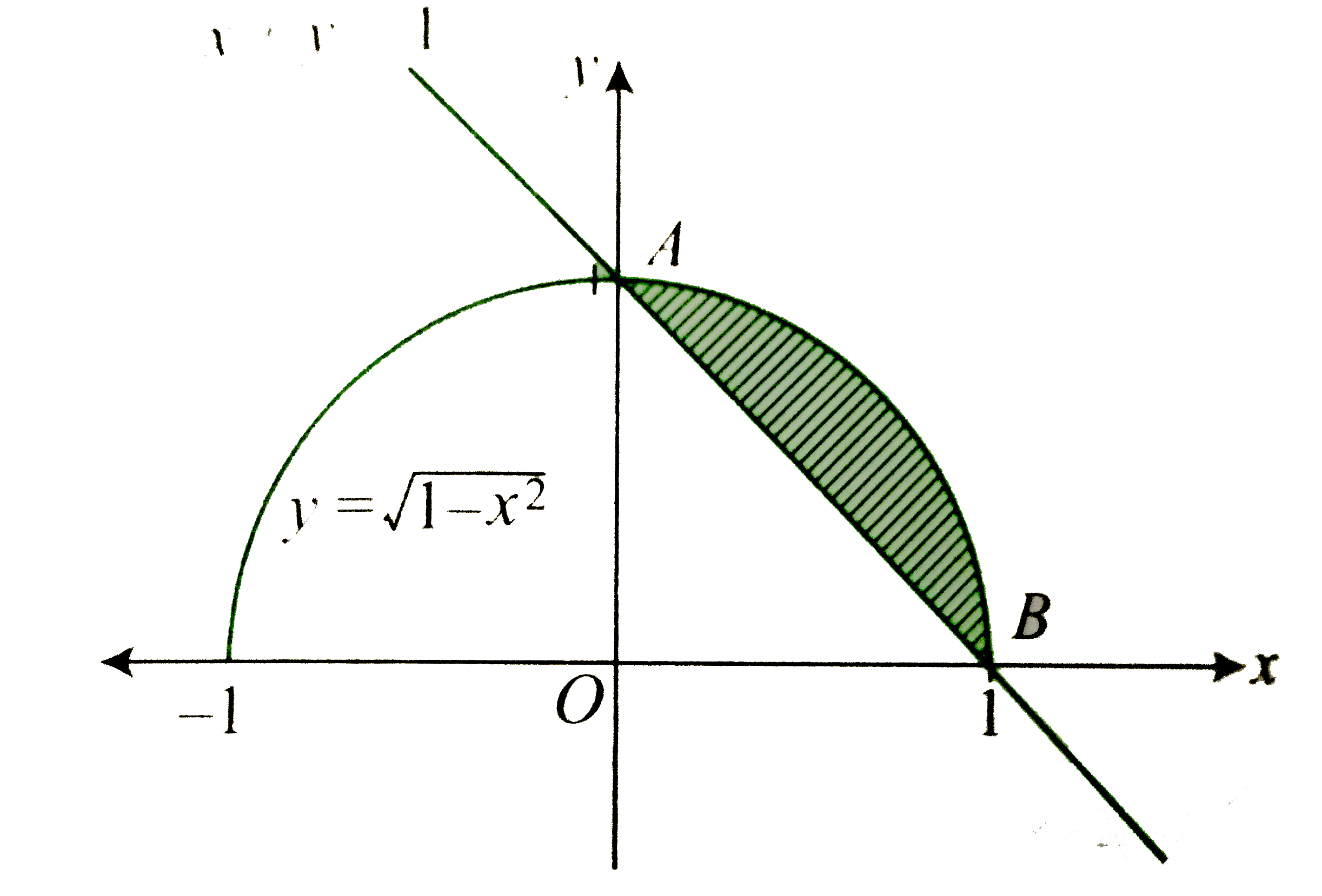
Area of the shaded region
=Area of quarter of the circle - Area of triangle OAB
=14×π(1)2−12×1×1=π−24
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Single Correct Answer Type27videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Multiple Correct Answer Type3videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year10videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
The area enclosed between the curve y=sin2xandy=cos2x in the interval 0≤x≤π is _____ sq. units.
06:31View SolutionIf the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
02:00View SolutionThe area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
04:34View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
04:53View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
03:24View SolutionLet f:(0,∞)−−−→0,∞ be a differentiable function satisfying, ξntx0(1−t)f(t)dt=∫x0tf(t)dtx∈R+andf(1)=1. Determine f(x).
05:30View SolutionLet f:[0,∞)→R be a continuous strictly increasing function, such that f3(x)=∫x0t.f2(t)dt for every x≥0. Then value of f(6) is_______
02:50View SolutionLet f:(0,∞)→R be given by f(x)=∫x1xe−(t+1t)dtt, then (a)f(x) is monotonically increasing on [1,∞) (b)f(x) is monotonically decreasing on (0,1) (c)f(2x) is an odd function of x on R
08:25View SolutionA continuous function f:R→R satisfies the equation f(x)=x+∫10f(t)dt. Which of the following options is true ?
01:49View SolutionLet f:[a,b]→[1,∞) be a continuous function and let g:R→R be defined as
g(x)=⎧⎪ ⎪⎨⎪ ⎪⎩0ifx<a∫xaf(t)dtifa≤x≤b∫baf(t)dtifx>b ThenView SolutionLet f:[0,∞)→R be a continuous function such that f(x)=1−2x+∫x0ex−tf(t)dt for all x∈[0,∞). Then, which of the following statements(s) is (are)) TRUE?
04:25View Solutionमाना [0,∞] में एक वास्तविक फलन f,f(x)=logx+∫x0√1+sint.dt द्वारा परिभाषित है। तब सिद्ध कीजिए की सभी x∈[0,∞] के लिए fn(x) का अस्तित्व होगा।
03:47View SolutionLet f:(0,∞)∈R be given
f(x)=∫x1/xe−(t+1t)1tdt, then04:10View SolutionIf ∫x0f(t)dt=x2+2x−∫x0tf(t)dt,x∈(0,∞). Then, f(x) is
03:58View SolutionConsider the function f:(−∞,∞)→(−∞,∞) defined by f(x)=x2−ax+1x2+ax+1;0<a<2. Let g(x)=∫ex0f'(t)1+t2 dt. Which of the following is true?
08:45View SolutionLet, f:(0,∞)→R be given by
f(x)=∫x1xe−(t+1t)dtt
Then02:37View Solution

