For a point P in the plane, let d1(P)andd2(P) be the distances of point P from the lines x−y=0andx+y=0, respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is ________. Solution in Tamil
The correct Answer is:6
For P(x,y), we have
2≤d1(P)+d2(P)≤4
⇒ 2≤|x−y|√2+|x+y|√2≤4
⇒ 2√2≤|x−y|+|x+y|≤4√2
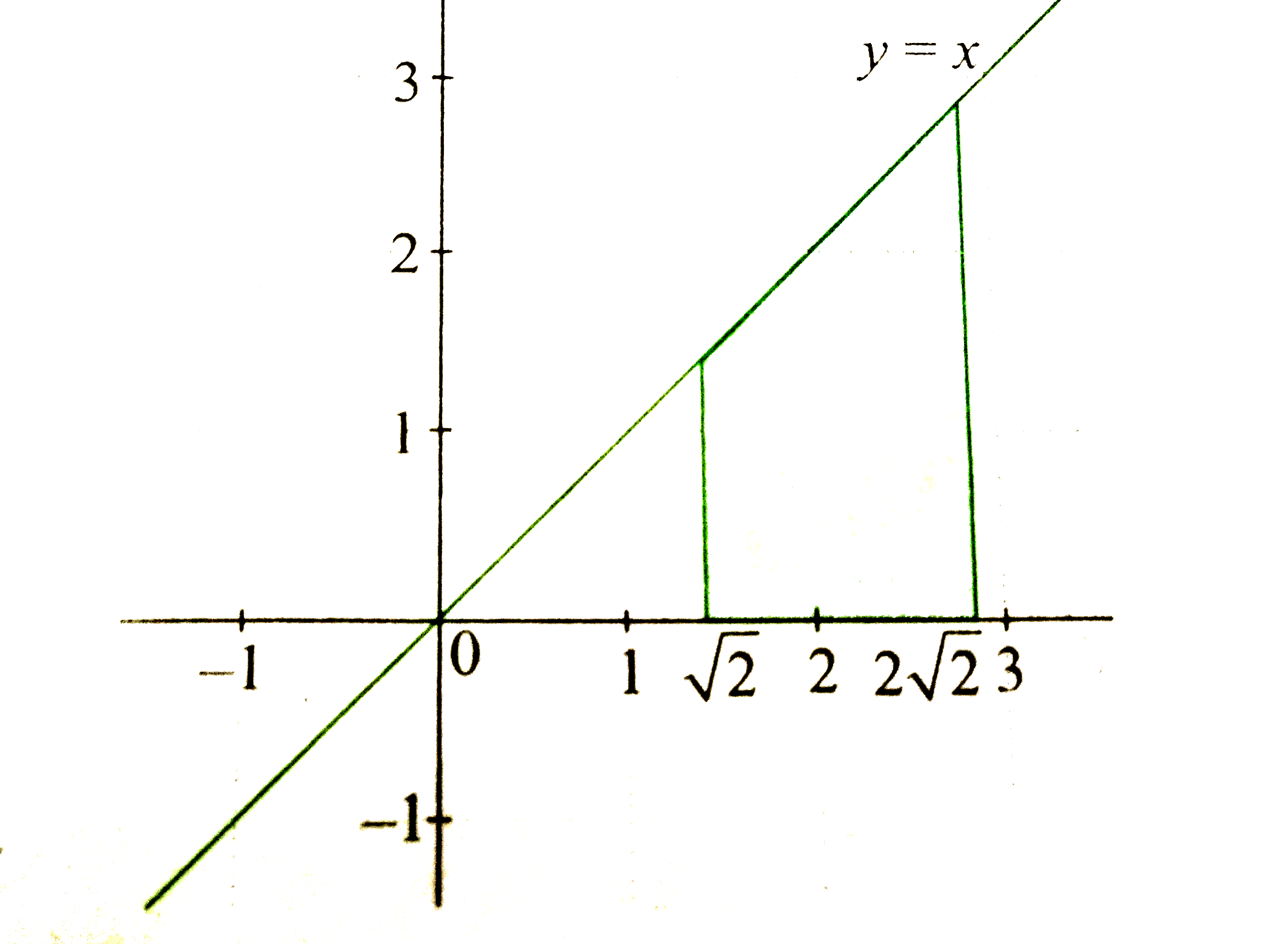
IN first quadrant if x>y, we have
2√2≤x−y+x+y≤4√2
or √2≤x≤2√2
The region of points satisfying these inequalities is
In first quadrant if x<y, we have
2√2≤y−x+x+y≤4√2
or √2≤y≤2√2
The region of points satisfying these inequalities is
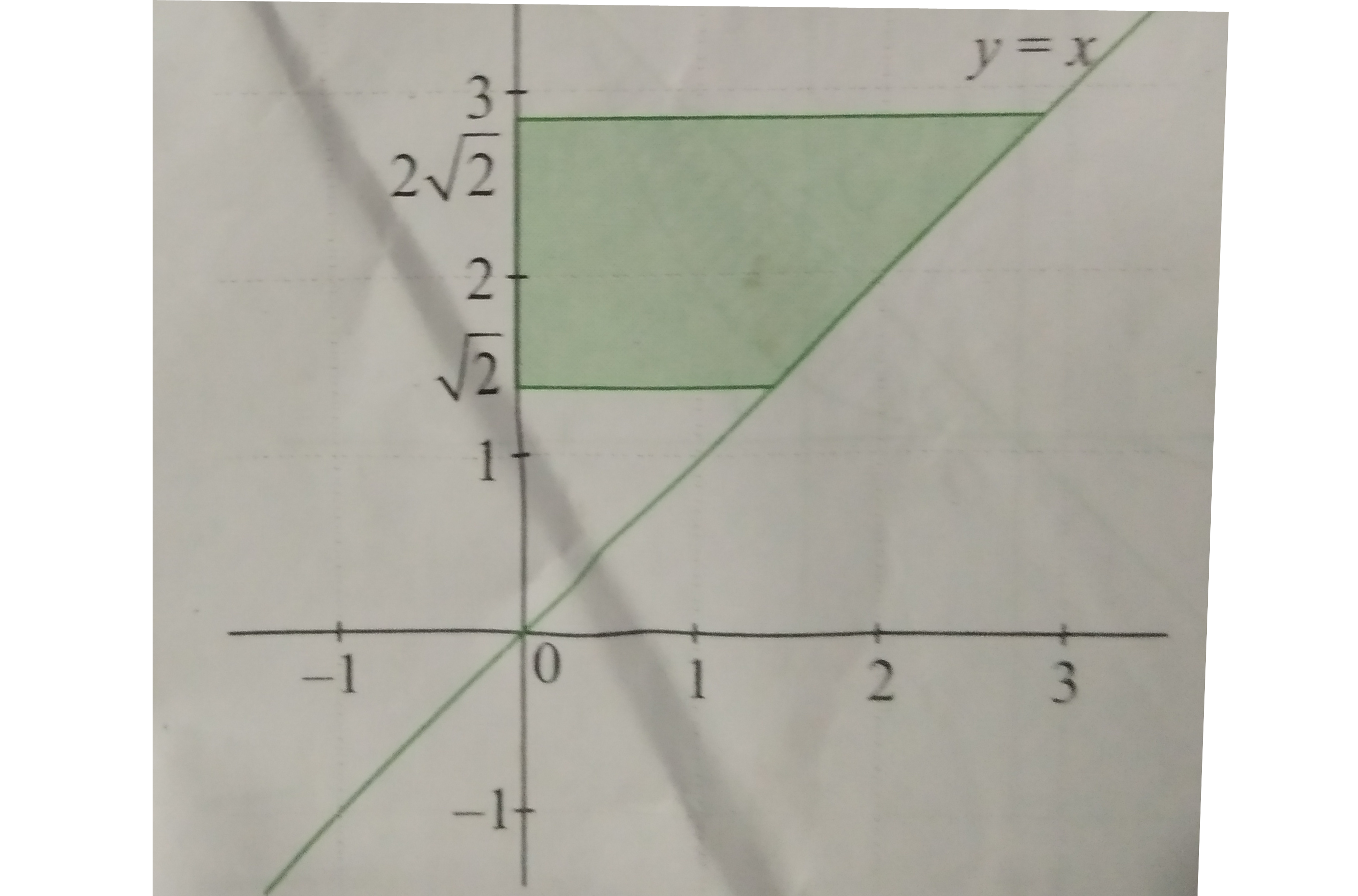
Combining above two regions we have

Area of the shaded region =((2√2)2−(√2)2)
=8−2=6 sq. units
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Single Correct Answer Type27videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Multiple Correct Answer Type3videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year10videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
The area enclosed between the curve y=sin2xandy=cos2x in the interval 0≤x≤π is _____ sq. units.
06:12View SolutionIf the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
04:55View SolutionThe area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
07:26View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
04:07View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionFor a point P in the plane, let d1 (P) and d2 (P) be the distance of the point P from the lines x – y = 0 and x + y = 0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2 < d1(P) + d2 (P)< 4, is
07:32View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionIf D_(p)=det[[p,15,8p^(2),35,9p^(2),35,9p^(3),25,10]] then D_(1)+D_(2)+D_(3)+D_(4)+D_(5)=
View SolutionLet three be two consumers in the market. Their demand functions are given. Calculate market dd.
d1(P)=30−P for P≤30 and d1(P)=0 for P<30
d2(P)=50−P for P≤50 and d2(P)=0 for P<5007:14View SolutionFor a point P in the plane let d1(P)andd2 be the distance of the point P from the lines x−y=0 R consisting of all points P lying in the first quadrant of the plane and satisfying 2≥d1(P)+d2(P)≥4, is
04:07View SolutionFor a point P in the plane, let d1(P) and d2(P) be the distances of the point P from the lines x−y=0 and x+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
10:46View SolutionA point p(x,y) moves in xy plane in such a way that √2≤|x+y|+|x−y|≤2√2. Area of the region representing all possible positions of the point 'p' is equal to :
06:55View SolutionGiven four parallel lines L1,L2,L3andL4 Let the distacnes between them be d12,d23,d34 respectively. Let P be a point sum of whose distances from four lines is K (d12<d23>d34) . Then the locus of the point P
 07:14View Solution
07:14View Solutionसमतल में स्थित किसी बिन्दु P से रेखाओ x - y = 0 तथा x + y = 0 की दुरी क्रमशः d1(P) तथा d2(P) है। यदि क्षेत्र R उन सभी बिन्दुओ P से बना है जो प्रथम चतुर्थांश (quadrant) में स्थित है तथा 2≤d1(P)+d2(P)≤4 को संतुष्ट करते है, तब क्षेत्र R का क्षेत्रफल है
04:07View Solutionयदि Dp=∣∣ ∣ ∣∣p158p2359p32510∣∣ ∣ ∣∣ तो D1+D2+D3+D4+D5=
04:07View SolutionFor a point P in the XY plane.Let d1(p),d2(p) and d3(p) be the distances of the point P from the x axis,y axis and x−y=0 respectively. If A is area of the region R consisting of all points P lying in the XY plane and satisfying d1(P)+d2(P)+√2d3(P)=5 then Which of the following is/are CORRECT
07:14View Solution

