Prove that cosθ⋅cosecθ=cotθSolution in Tamil
The correct Answer is:A, D
For α=1
y=|x−1|+|x−2|+x=⎧⎪⎨⎪⎩3−xx<11+x1≤x<23x−3x≥2
For α=0,y=3
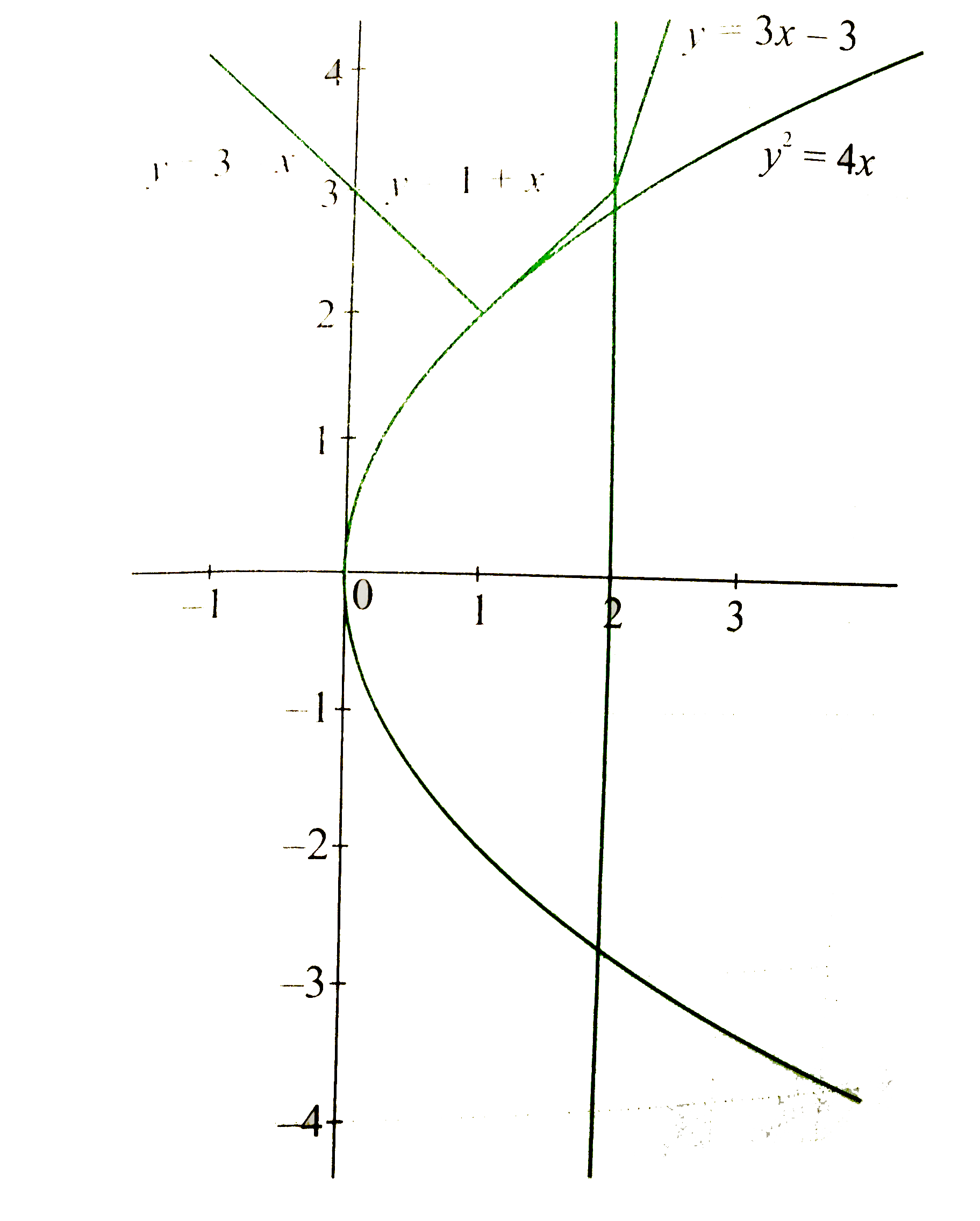
A=12(2+3)×1+12(2+3)×1−2∫02√xdx
⇒ A=5−83√2
∴ F(1)+83√2=5
For α=0,y=|−1|+|−2|=3
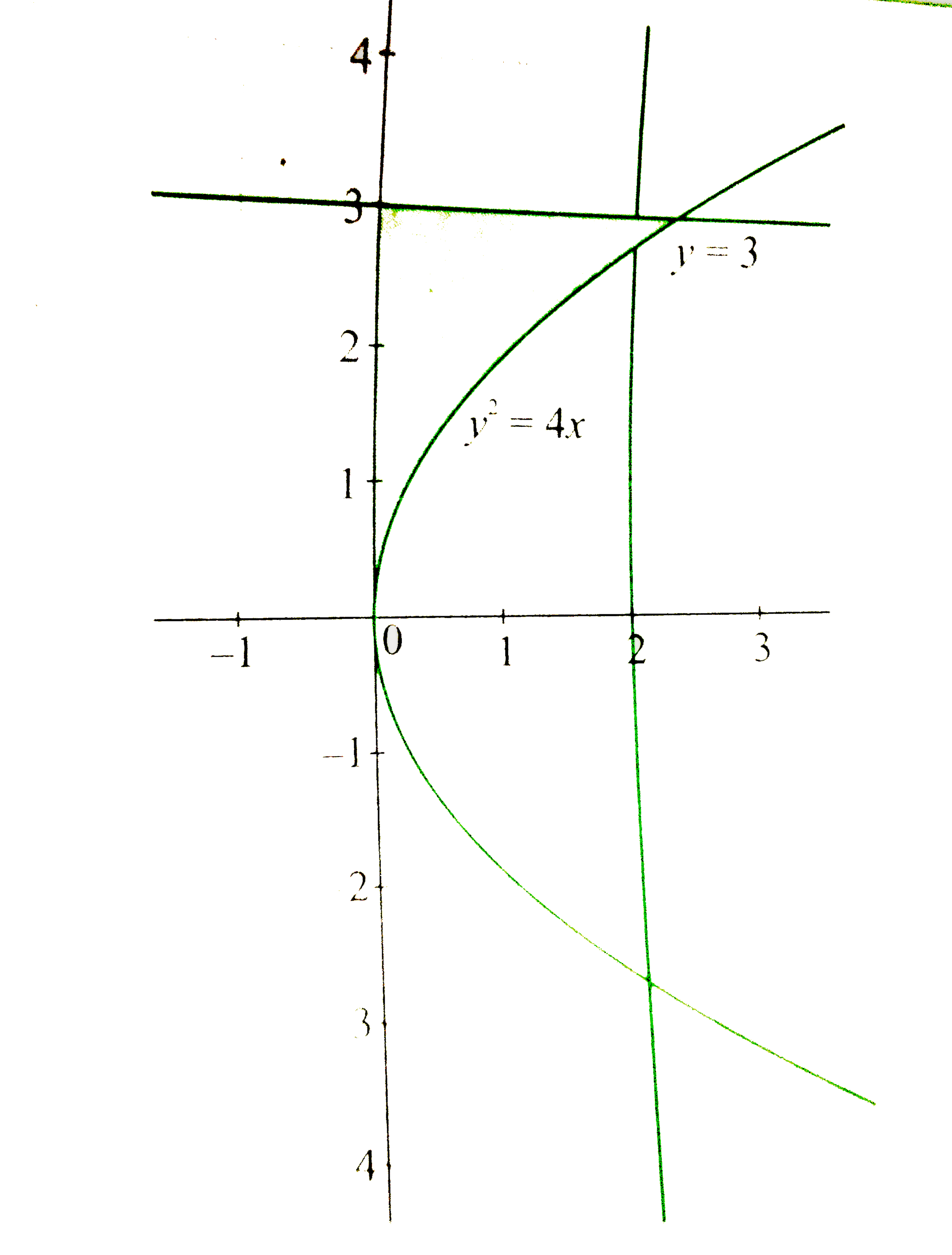
A=6−2∫02√xdx
⇒ A=6−83√2
∴ F(0)+83√2=6
Note : Solutions of the remaining parts are given in their respective chapters.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Single Correct Answer Type27videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Multiple Correct Answer Type3videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year10videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
The area enclosed between the curve y=sin2xandy=cos2x in the interval 0≤x≤π is _____ sq. units.
02:54View SolutionIf the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
02:45View SolutionThe area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
03:39View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
04:01View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
01:53View Solutioncosθ1−tanθ + sinθ1−cotθ is equals to
02:42View SolutionProve that : (cosecθ−cotθ)2 = 1+cosθ1−cosθ
03:09View SolutionIf 2cos^(2) θ - 5cosθ +2 =0 , 0^circ lt θ lt 90^circ , then the value of (cosecθ + cotθ) is:
01:26View SolutionIf ((sinθ−cosecθ)(cosθ−secθ))/(tan^(2)θ -sin^(2)θ) = r^3 , then r=? यदि ((sinθ−cosecθ)(cosθ−secθ))/(tan^(2)θ -sin^(2)θ) = r^3 है तो r बराबर हैः
01:09View SolutionIf sqrt((1-cosθ)/(1+cosθ)) xx sqrt((cosecθ -cot θ)/(cosecθ +cot θ))= (1-r)/(1+r) , then the value of r is: यदि sqrt((1-cosθ)/(1+cosθ)) xx sqrt((cosecθ -cot θ)/(cosecθ +cot θ))= (1-r)/(1+r) है तो r का मानहैः
08:32View SolutionThe value of (sinθ−cosθ)(1+tanθ+cotθ)1+sinθcosθ = ? (sinθ−cosθ)(1+tanθ+cotθ)1+sinθcosθ का मान है :
03:09View SolutionThe value of (1+cotθ–cosecθ)(1+cosθ+sinθ)secθ = ? (1+cotθ–cosecθ)(1+cosθ+sinθ)secθ का मान है :
01:34View Solutioncosθ/ (1-tanθ) + sinθ/ (1−cotθ) is equals to
02:43View SolutionProve that : (cosecθ−cotθ)^2 = (1-cosθ)/(1+cosθ)
04:58View SolutionIf a2+b2+c2=1,
∣∣ ∣ ∣∣a2+(b2+c2)cosθab(1−cosθ)ac(1−cosθ)ba(1−cosθ)b2(c2+a2)cosθbc(1−cosθ)ca(1−cosθ)cb(1−cosθ)c2+(a2+b2)cosθ∣∣ ∣ ∣∣
then prove that the value of determinant is independent of a,b,c?01:31View Solution

