Let A,B,C be angles of triangles with vertex $A \equiv (4, - 1)$ and internal angular bisectors of angles B and C be $x - 1 = 0$ and $x - y - 1 = 0$ respectively.
Slope of BC is

A

$1 / 2$

B

2

C

3

D

12

Text Solution

Verified by Experts

The correct Answer is:B

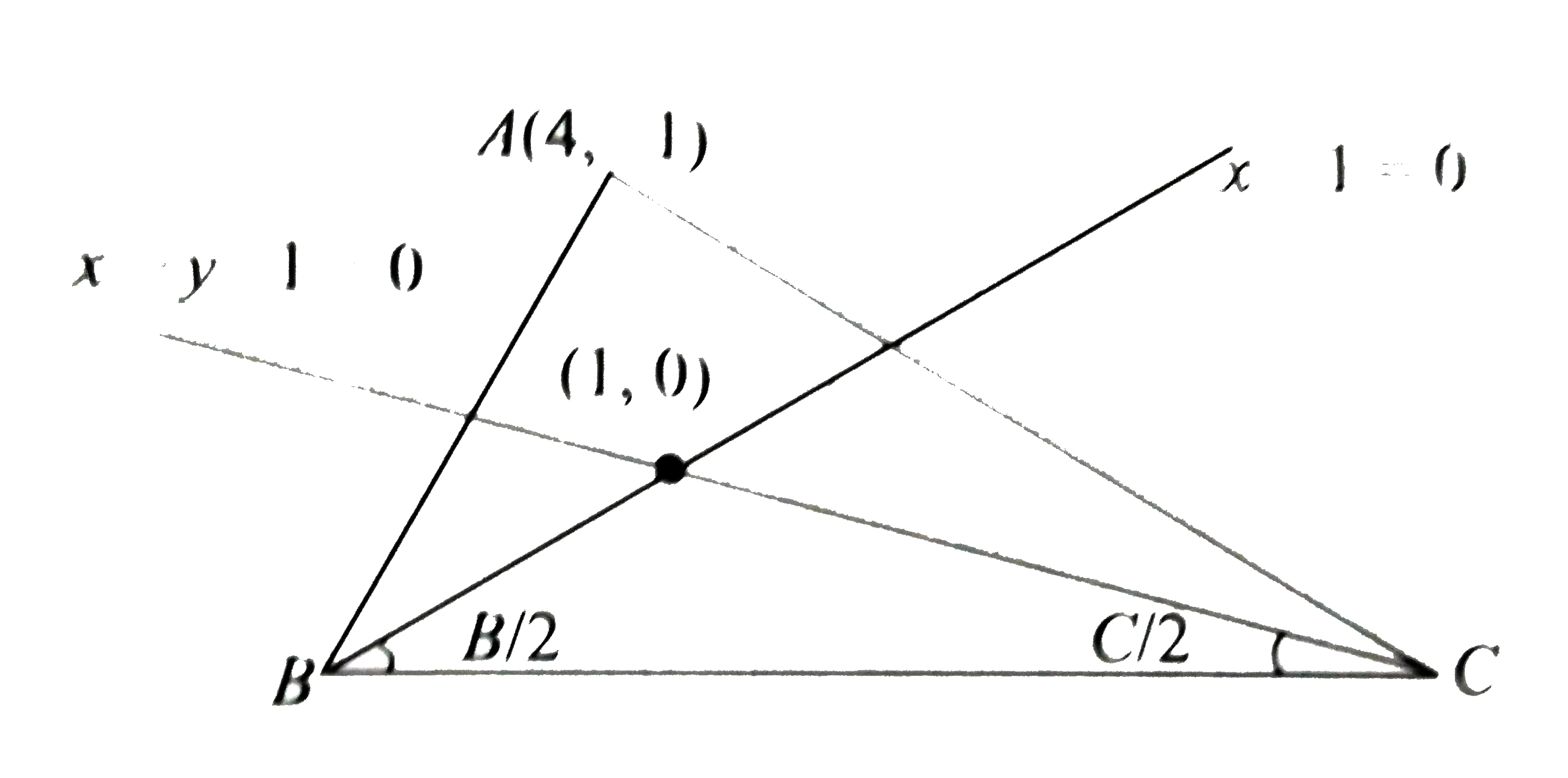
Image of $A (4, - 1)$ in bisectors of B and C lies on side BC
$\Rightarrow$ Image of $A (4, - 1)$ with respect to $x - y - 1 = 0$ is
$\frac{x - 4}{1} = \frac{y + 1}{- 1} = - \frac{2 (4 + 1 - 1)}{2} \Rightarrow (0, 3)$
Image of $A (4, - 1)$ with respect to $x - 1 = 0$ is
$\frac{x - 4}{1} = \frac{y + 1}{0} = - \frac{2 (4 - 1)}{1} \Rightarrow (- 2, - 1)$
Hence, slope of BC is $m = (\frac{3 + 1}{0 + 2}) = 2$

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let A,B,C be angles of triangles with vertex $A \equiv (4, - 1)$ and internal angular bisectors of angles B and C be $x - 1 = 0$ and $x - y - 1 = 0$ respectively.
If A,B,C are angles of triangle at vertices A,B,C respectively then $cot (\frac{B}{2}) cot . (\frac{C}{2}) =$
A2
B3
C4
D6
Consider a triangle ABC with vertex $A (2, - 4)$ . The internal bisectors of the angle B and C are $x + y = 2$ and $x - 3 y = 6$ respectively. Let the two bisectors meet at $I$ .
If $(x_{1}, y_{1}) and (x_{2}, y_{2})$ are the co-ordinates of the point B and C respectively, then the value of $(x_{1} x_{2} + y_{1} y_{2})$ is equal to :
A4
B5
C6
D8
Consider a triangle ABC with vertex $A (2, - 4)$ . The internal bisectors of the angle B and C are $x + y = 2$ and $x - 3 y = 6$ respectively. Let the two bisectors meet at $I$ .
If $(x_{1}, y_{1}) and (x_{2}, y_{2})$ are the co-ordinates of the point B and C respectively, then the value of $(x_{1} x_{2} + y_{1} y_{2})$ is equal to :
A4
B5
C6
D8

CENGAGE-STRAIGHT LINE-Comprehension Type

Home
Ask Doubt
Profile