In a ΔABC,A=(2,3) and medians through B and C have equations x+y−1=0 and 2y−1=0
Equation of side BC is

A

5x+13y+11=0

B

5x−3y=1

C

5x=3y

D

5x+13y−11=0

Text Solution
Verified by Experts

The correct Answer is:A

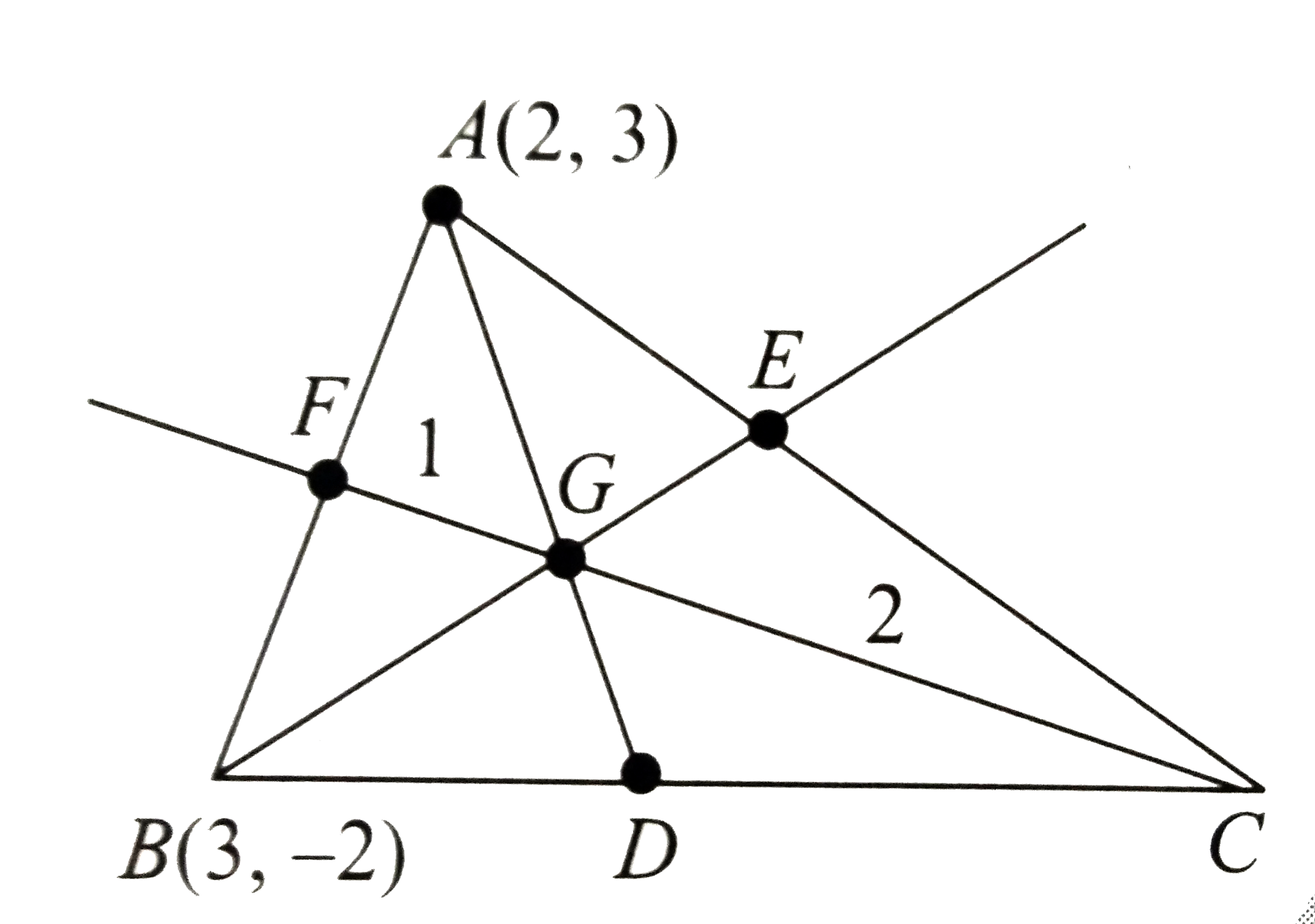
ocr_image
Centroid is the point of intersection of x+y−1=0,2y−1=0 or D(12,12)
Slope of AD is 3−122−12=53
∴ Equation of AD is y−3=53(x−2) or 5x−3y−1=0
A point of CF:2y−1=0 is (α,12)
Let this be the midpoint of AB.
∴ B is (2α−2,−2) which lies on median BE:x+y−1=0
∴2α−2−2−1=0∴α=52
∴B(3,−2)
G divides CF in 2:1
∴C=(−72,12)
∴ Equation of BC is y+212+2=x−3−72−3
or y+25=x−3−13
or 5x+13y+11=0

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSSTRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In a ΔABC,A=(2,3) and medians through B and C have equations x+y−1=0 and 2y−1=0
    Equation of median through A is

    Ax+y=4
    B5x−3y=1
    C5x+3y=1
    D5x=3y

  • In an equilateral triangle ABC, equation of the sides BC is x+y−2=0 and the centroid of ΔABC is (0, 0). If points A, B and C are in anticlockwise order, then the equation of side AC is

    A(y+2)=(2−√3)(x+2)
    B(y+2)=(2+√3)(x+2)
    C(y+1)=(2+√3)(x+1)
    Dx+2=0

  • In a triangle ABC, coordinate of A are (1,2) and the equations of the medians through B and C are respectively, x+y=5&x=4. Then area of ΔABC (in sq. units) is:

    A12
    B9
    C4
    D5