If C1:x2+y2=(3+2√2)2 is a circle and PA and PB are a pair of tangents on C1, where P is any point on the director circle of C1, then the radius of the smallest circle which touches c1 externally and also the two tangents PA and PB is 2√3−3 (b) 2√2−1 2√2−1 (d) 1Solution in Tamil
1
2
3
4
The correct Answer is:A
Let Q be the centre of the given circle and R be the centre of the smallest circle touching the given circle externally. Then
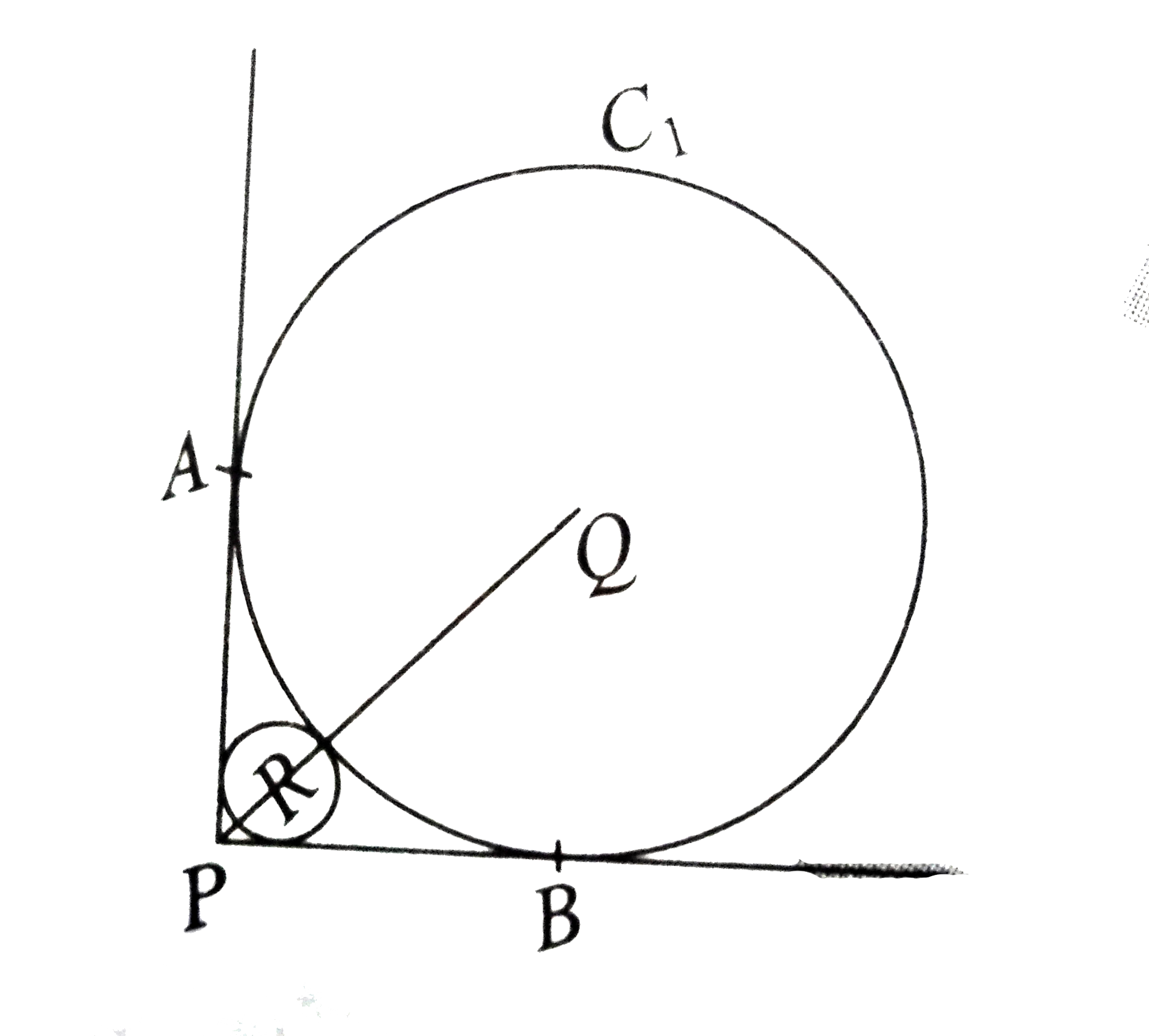
AQ=3+2√2
PQ=3√2+4
Let radius of smaller circle is r.
⇒3√2+4=QR+RP=3+2√2+r+r√2(∵∠APQ=π4)
⇒(√2+1)=r(√2+1)=r=1
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type9videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE6videos
CIRCLE
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year14videos
COMPLEX NUMBERS
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
03:01View SolutionIn the diagram as shown, a circle is drawn with centre C(1, 1) and radius I and a line L. The line Lis tangential to the circle at Q. Further L meet the y-axis at R and the x-axis at Pis such a way that the angle OPQ equals θ where 0<θ<π2 The coordinates of Q are
01:55View SolutionFind the derivative of y=ln(cosx2).
06:02View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
05:36View SolutionC1 is a circle of radius 1 touching the x- and the y-axis. C2 is another circle of radius greater than 1 and touching the axes as well as the circle C1 . Then the radius of C2 is 3−2√2 (b) 3+2√2 3+2√3 (d) none of these
02:11View SolutionIf C1:x2+y2=(3+2√2)2 is a circle and PA and PB are a pair of tangents on C1, where P is any point on the director circle of C1, then the radius of the smallest circle which touches c1 externally and also the two tangents PA and PB is 2√3−3 (b) 2√2−1 2√2−1 (d) 1
02:44View SolutionIf PandQ are two points on the circle x2+y2−4x+6y−3=0 which are farthest and nearest respectively from the point (7,2) then. (A) P≡(2−2√2,−3−2√2) (B) Q≡(2+2√2,−3+2√2) (C) P≡(2+2√2,−3+2√2) (D) Q≡(2−2√2,−3+2√2)
04:27View SolutionIf C1:x2+y2=(3+2√2)2 be a circle. PA and PB are pair of tangents on C1 where P is any point on the director circle of C1, then the radius of the smallest circle which touches C1 externally and also the two tangents PA and PB is
06:44View SolutionTwo circles C1 and C2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB and QY meets circles C1 andC2 at Xa n dZ respectively. Then prove that Y is the midpoint of XZ
03:35View SolutionConsider three circles C1,C2andC3 such that C2 is the director circle of C1,andC3 is the director circle of C2. Tangents to C1, from any point on C3 intersect C2, at PandQ. Find the angle between the tangents to C2 at P and Q. Also identify the locus of the point of intersec- tion of tangents at PandQ.
03:12View SolutionC1 is a circle of radius 1 touching the x- and the y-axis. C2 is another circle of radius greater than 1 and touching the axes as well as the circle C1 . Then the radius of C2 is (a)3−2√2 (b) 3+2√2 3+2√3 (d) none of these
05:32View SolutionIf C1:x2+y2=(3+2√2)2 is a circle and PA and PB are a pair of tangents on C1, where P is any point on the director circle of C1, then the radius of the smallest circle which touches c1 externally and also the two tangents PA and PB is
(a) 2√3−3 (b) 2√2−1 2√2−1 (d) 104:15View SolutionIf C1:x2+y2=(3+2√2)2 be a circle. PA and PB are pair of tangents on C1 where P is any point on the director circle of C1, then the radius of the smallest circle which touches C1 externally and also the two tangents PA and PB is
01:11View SolutionA circle C1, of radius 2 touches both x-axis and y- axis. Another circle C1 whose radius is greater than 2 touches circle and both the axes. Then the radius of circle is (a) 6−4√2 (b) 6+4√2 (c) 3+2√3 (d) 6+√3
03:18View SolutionIf PandQ are two points on the circle x2+y2−4x+6y−3=0 which are farthest and nearest respectively from the point (7,2) then.
(A) P≡(2−2√2,−3−2√2)
(B) Q≡(2+2√2,−3+2√2)
(C) P≡(2+2√2,−3+2√2)
(D) Q≡(2−2√2,−3+2√2)04:55View SolutionC1 is a circle of radius 1 touching the x- and the y-axis. C2 is another circle of radius greater than 1 and touching the axes as well as the circle C1 . Then the radius of C2 is (a)3−2√2 (b) 3+2√2 (c)3+2√3 (d) none of these
03:35View Solution

