Two equal circles of largest radii have following property:
(i) They intersect each other orthogonally,
(ii) They touch both the curves 4(y+2)=x2 and 4(2−y)=x2 in the region x∈[−2√2,2√2]. Then radius of this circle is
A
√2
B
√3
C
1√3
D
32
Text Solution
The correct Answer is:A
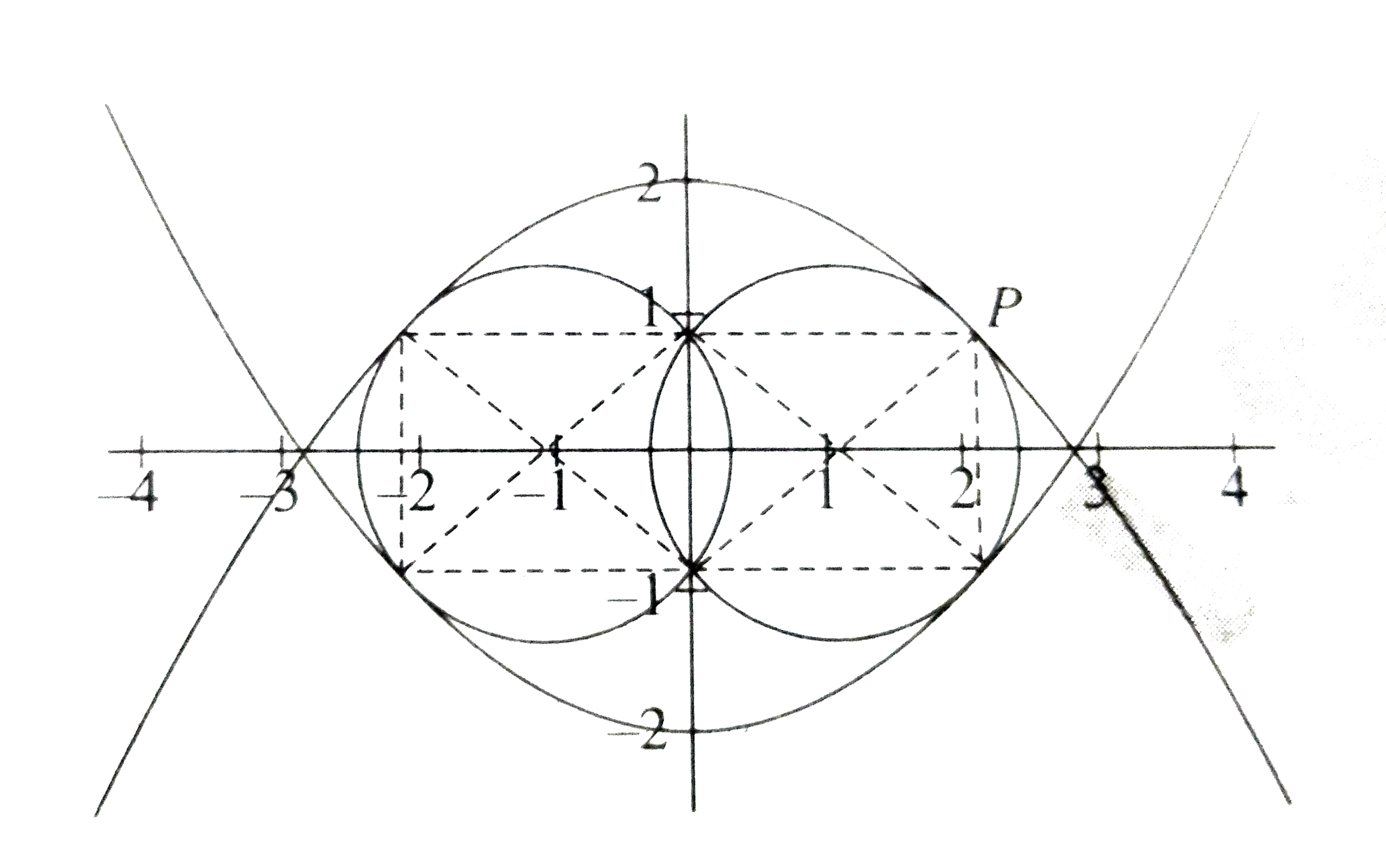
Let the radius of circle is r.
From geometry, P≡(r√2,r√2).
Now, this point lies on the curve 4(2−y)=x2
⇒4(2−r√2)=(r√2)2
⇒r=√2
|
Topper's Solved these Questions
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type
10 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Comprehension Type
1 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - JEE Advenced Single Answer Type
18 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank
4 Videos
Similar Questions
Knowledge Check
If the line ax + y = c, touchs both the curves x2+y2=1
and y2=4√2x, then |c| is equal toA1√2B2C√2D12If the line ax+y=c, touches both the curves x2+y2=1andy2=4√2x, then |c| is equal to:
A12B√2C2D1√2The two circles x2+y2−cx=0andx2+y2=4 touch each other if:
A|c|=4B|c|=2C|c|=8DNone of these
Equation of the circle of minimum radius which touches both the parabolas y=x2+2x+4 and x−y2+2y+4 is
View SolutionThe radius of the circle touching the line x+y=4 at (1,3) and intersecting x2+y2=4 orthogonally is
View SolutionThe equation of the circle which cuts each of the three circles x2+y2=4,(x−1)2+y2=4andx2+(y−2)2=4 orthogonally is
View SolutionThe radius of the circle touching the line x+y=4 at (1,3) and intersecting x2+y2=4 orthogonally is
View Solutionx=1 is the radical axis of two of the circles which intersect orthogonally. If the equation of one of the circles is x2+y2=4, then the equation of the other circle is
View Solution
