The following figure shows the graph of a continuous function y = f(x) on the interval [1, 3]. The points A, B, C have coordinates (1,1), (3,2),(2,3), respectively , and the lines L1andL2 are parrallel, with L1 being tangent to the curve at C. If the area under the graph of y = f(x) from x = 1 to x = 3 is 4 square units, then the area of the shaded region is
![The following figure shows the graph of a continuous function y = f(x) on the interval [1, 3]. The points A, B, C have coordinates (1,1), (3,2),(2,3), respectively , and the lines L(1) and L(2) are parrallel, with L(1) being tangent to the curve at C. If the area under the graph of y = f(x) from x = 1 to x = 3 is 4 square units, then the area of the shaded region is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_CAL_DPP_9_2_E01_501_Q01.png)
Solution in Tamil
1
2
3
4
The correct Answer is:B
Equation of L2:y−1=2−13−1(x−1)
or 2y−2=x−1
2y−x=1
⇒ Slope of L2=1/2.
Equation of L1=y−3=12(x−2)
or 2y−x=4
∴ D(1,52)andE(3,72)
Area under f(x) = 4
∴ Shaded area = Area of trapezium DEFG - Area under f(x)
=12(52+72)×2−4
=6−4=2
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Multiple Correct Answer Type3videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Comprehension Type2videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year9videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
If the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
04:59View SolutionIn the following figure, the graphs of two functions y = f(x) and y = sin x are givne. They intersect at origin, A(a,f(a)),B(π,0)andC(2π,0).Ai(i=1,2,3) is the area bounded by the curves as shown in the figure, respectively, for x∈(0,a),x∈(a,π),x∈(π,2π).
If A1=1+(a−1)cosa−sin a, then
The function f(x) isView SolutionFind the area bounded by the curves x+2|y|=1 and x=0.
08:43View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
04:23View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
04:43View SolutionGraph of a function y=f(x) is shown in the adjacent figure.Four limits l_(1),l_(2),l_(3) and I_(4), are given as:
08:25View SolutionThe following shows the graph of a continuous function y=f(x)on the interval [1,3]. The points A, B, C have coordinates (1,1),(3,2),(2,3) respectively, and the lines L1 and L2 are parallel, with L1 being tangent to the curve at C. If the area under the graph of y=f(x) from x=1 to x=3 is 4 square units, then the area of the shaded region is -
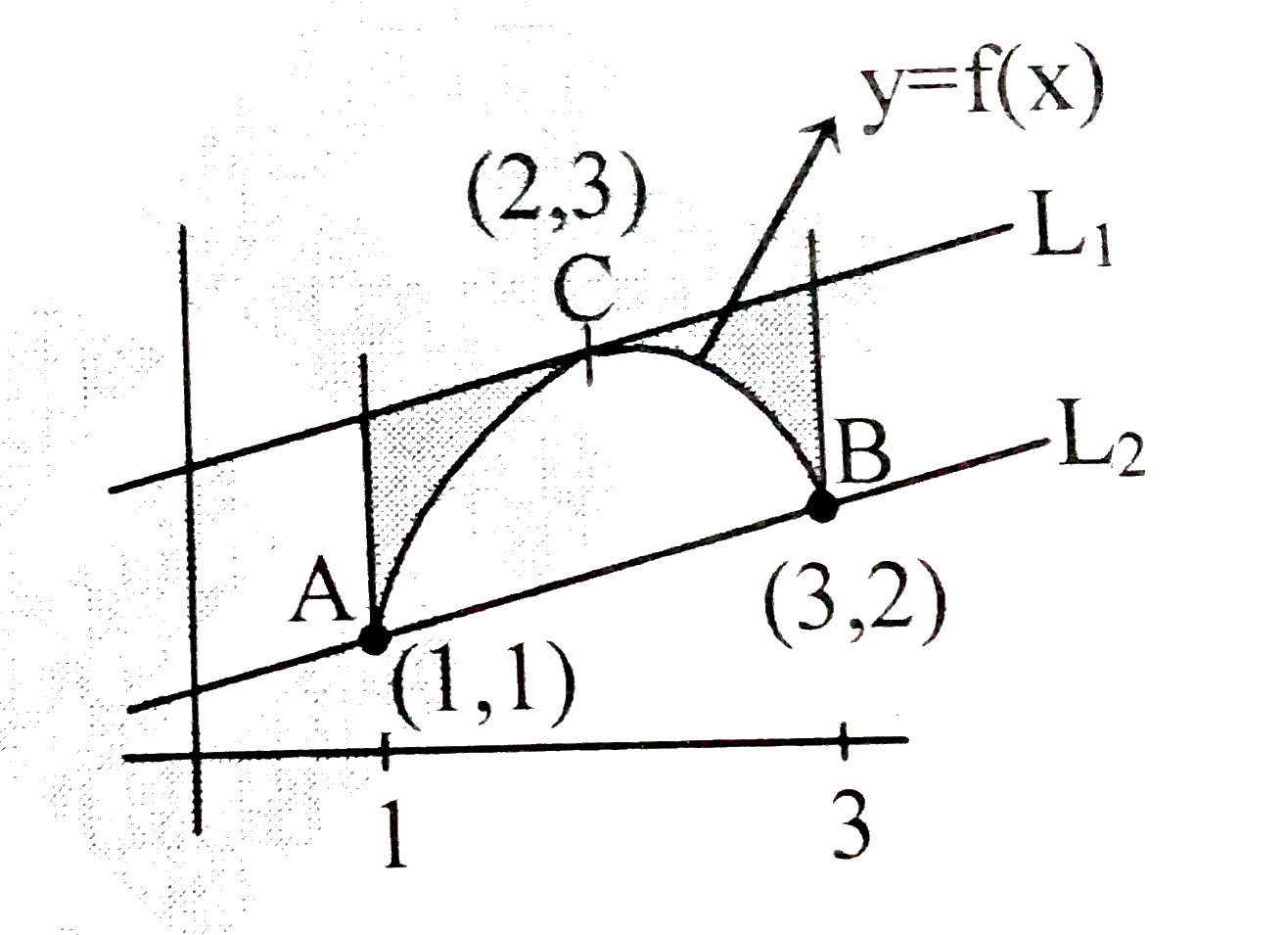05:34View SolutionL1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
The lines L1 and L2 are -02:15View SolutionL1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
The lines L1 and L2 intersect at the point07:59View SolutionL1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
Equation of plane containinng L1 and L2 is -04:06View SolutionThe line L1:x5+yb=1 passes through the point (13, 32) and is parallel to L2:xc+y3=1. Then, the distance between L1andL2 is
07:05View SolutionConsider the lines
L1:x+y=10, L2:x+y=60
L3:x=40, L4:y=40.
L1 meets x - axis and y - axis at A and B respectively.
L4 meets y - axis at C and L2 at D
L3 meets L2 at E and x-axis at F.
Perimeter of the hexagon ABCDEF is02:36View SolutionThe folloiwng figure shows the graph of a continuous function y = f(x) on the interval [1, 3]. The points A, B, C have coordinates (1,1), (3,2),(2,3), respectively , and the lines L1andL2 are parrallel, with L1 being tangent to the curve at C. If the area under the graph of y = f(x) from x = 1 to x = 3 is 4 square units, then the area of the shaded region is
07:59View SolutionThe following diagram shows the continuous function y = f (x) at the [1,3] interval. The coordinates of A, B, C are (1, 1), (3, 2) and (2, 3) respectively: L_1 And L_2 The lines are parallel, L_1 Is the tangent line that touches the curve at C. If y = f (x) the area under the graph is 4 square units from x = 1 to x = 3, then what is the area of the covered area?
14:00View Solutionएक रेखा L1:x5+yb=1 , बिन्दु M(13, 32) से गुजरती है। रेखा L2:xc+y3=1 रेखा L1 के समान्तर है, तो L1 एवं L2 के मध्य दुरी है
05:14View SolutionL1:x+1−3=y−32=z+21
L2:x1=y−7−3=z+72
रेखाएँ L1 व L2 है05:21View Solution