Find the coordinates of the point of inflection of the curve f(x) =e−x2Solution in Tamil
We have f(x) =e−x2
∴f(x)=−2xe−x2
⇒f(x)=−2e−x2.1+x.e−x2(−2x)
If f(x)=0 then 2e−x2(2x−1)=0
⇒x=+1√2
when x=+1√2,y=e−12=1√e
Thus the points of inflection are +1√2,1√e
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Illustration
2 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise 6.1
10 Videos
- METHODS OF DIFFERETIATIONBOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank
13 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
Let A={2,4,6},B={8,10,12,14} and f={(2,8),(4,10),(6,12)} be a function from A to B. Show that f is one to one but not onto function.
View SolutionProve that the following functions are strictly increasing: f(x)=log(1+x)−2x2+x
View SolutionLet f:(−5,5)→R be a differentiable function with f(4) = 1, f′(4)=1,f(0)=−1 and f^(')(0) = 1,Ifg(x) = f(2f^(2)(x)+2))^(2),then - g^(')(0) equals
View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?
View SolutionNumber of points of inflection for f(x)=x2e−|x| is 1 (b) 2 (c) 3 (d) 4
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
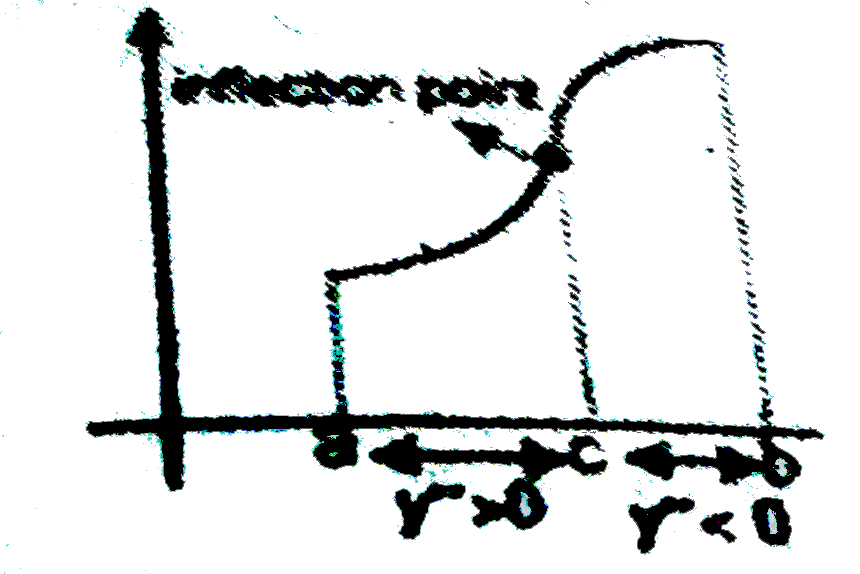
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionDraw the graph of f(x)=ex1+ex. Also find the point of inflection.
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionDraw the graph of f(X)=loge(1−logex). Find the point of inflection
View SolutionFind the inflection points of the curve y=(x−5)5/3+2 .
View SolutionDetermine the intervals of concavity of the curve f(x)=(x−2)3(x−4),x∈R and the points of inflection if any.
View SolutionA point of inflection of the curve y=e−x2 is
View SolutionIf x0 is the x - coordinate of the point of inflection of a curve y=f(x) then (second derivative exists) ………….. .
View SolutionDraw the graph of f(x)=ex1+ex. Also find the point of inflection.
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionDraw the graph of f(X)=loge(1−logex). Find the point of inflection
View Solution
