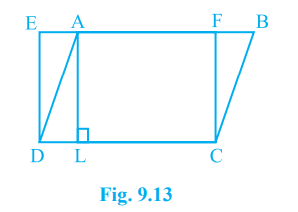
In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that (i) ar (ABCD) = ar (EFCD)
(ii) ar (ABCD) = DC × AL
Solution in Punjabi
Step by step video & image solution for In Fig. 9.13, ABCD is a parallelogram and EFCD is a rectangle. Also, AL bot DC. Prove that (i) ar (ABCD) = ar (EFCD) (ii) ar (ABCD) = DC × AL by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
I travelled 432 km by car and 48 litres of the petrol was consumed. I have to go at a place which is 180 km far. How much litres of the petrol is needed for it ?
05:03View SolutionThe centre of a circle lies in .............. of the circle.
05:41View SolutionABCD is a trapezium in which AB |DC,AB=16cm and DC=24cm. If E and Fare respectively the midpoints of AD and BC prove that ar(ABFE)=(9)/(11)ar(EFCD)
02:55View SolutionMatch the following Column A to Column B
04:04View Solutionआक्रति 9.13 में , ABCD एक समांतर चतुर्भुज है और EFCD एक आयत है ।
साथ ही , AL⊥DC है सिद्ध कीजिए कि
(i) ar(ABCD)=ar(EFCD)
(ii)(ABCD)=DC×AL
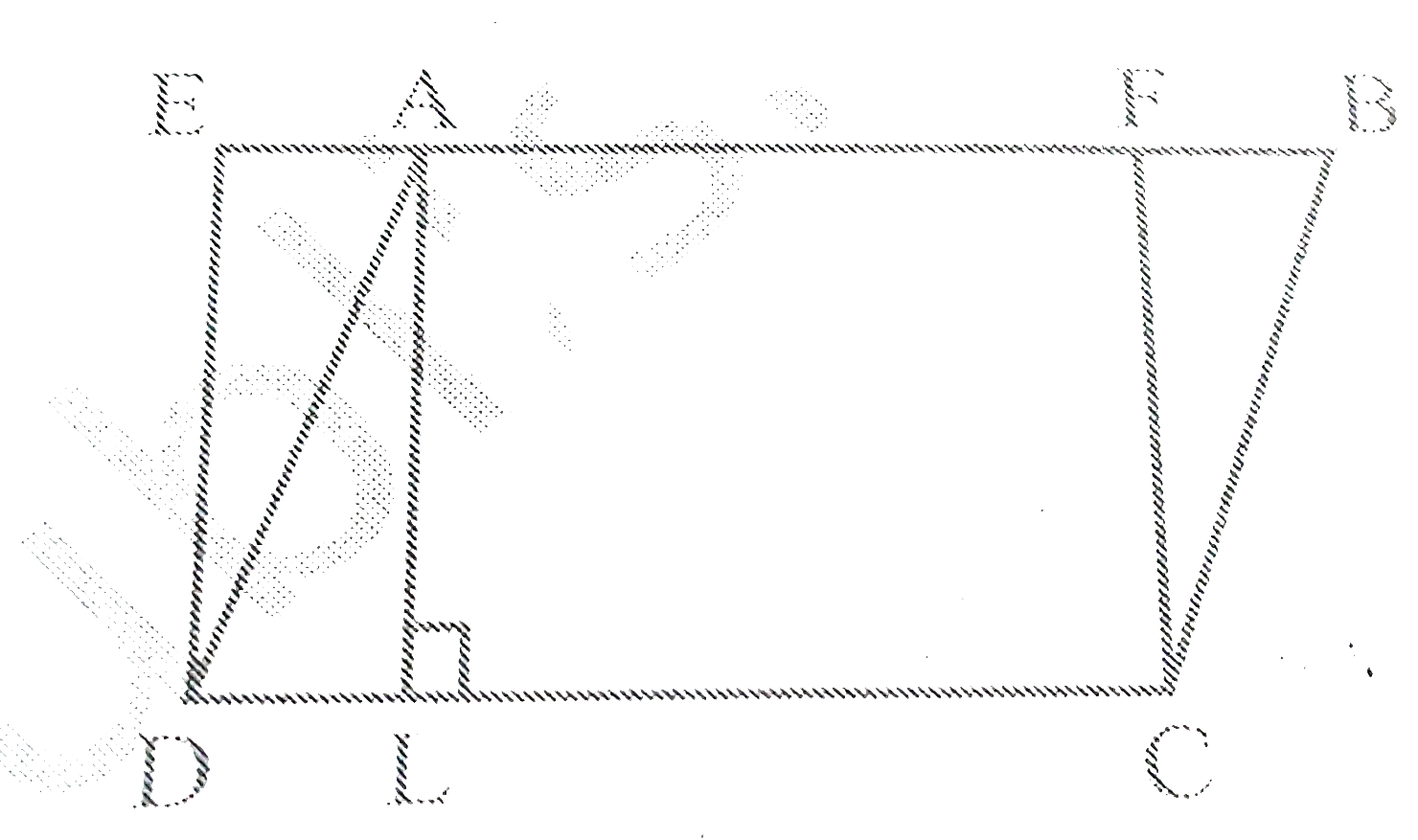
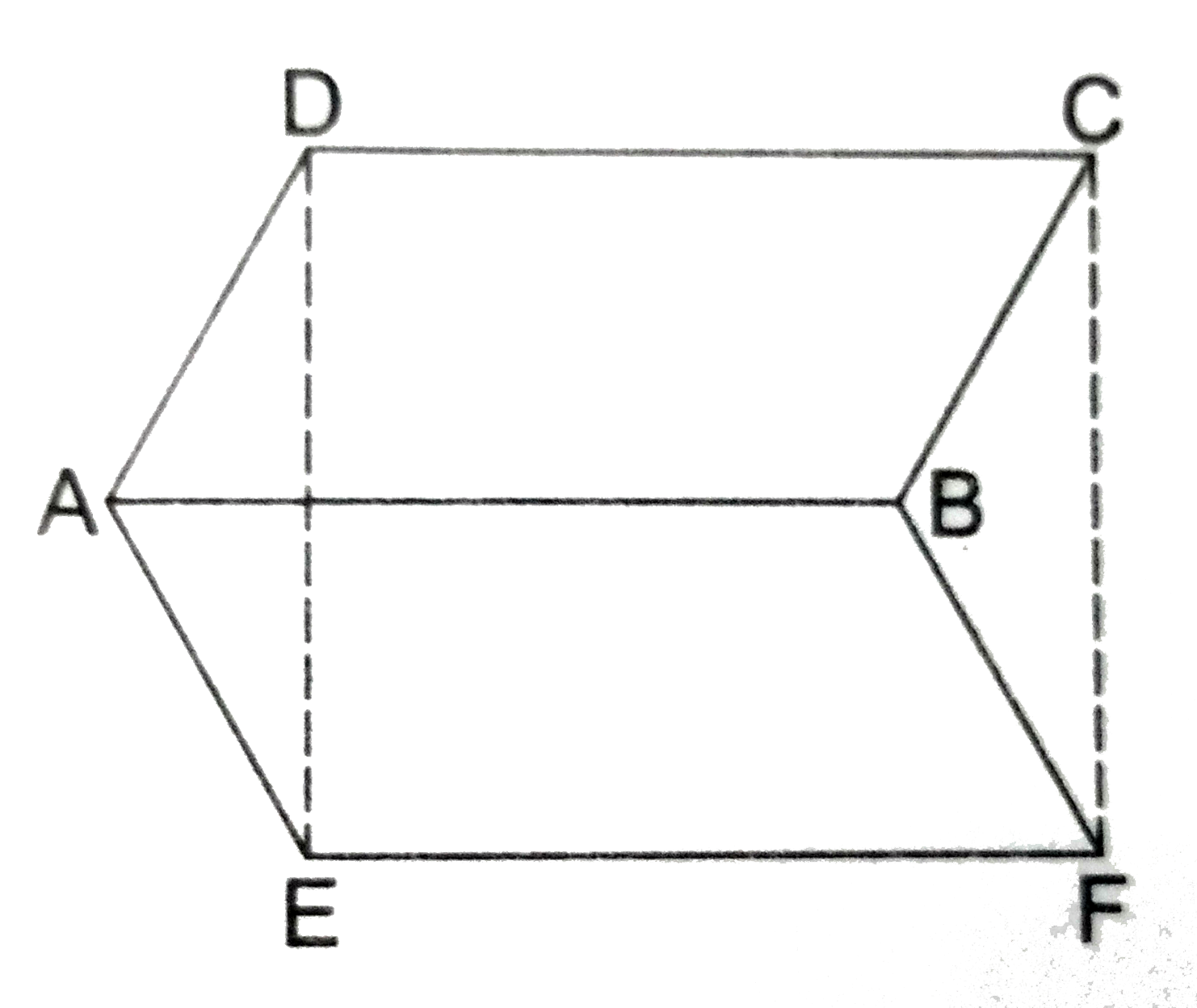
01:15View SolutionIn the adjoing figure, two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that
ar(||gm ABCD)+ar(||gm AEFB)
=ar(||gm EFCD).
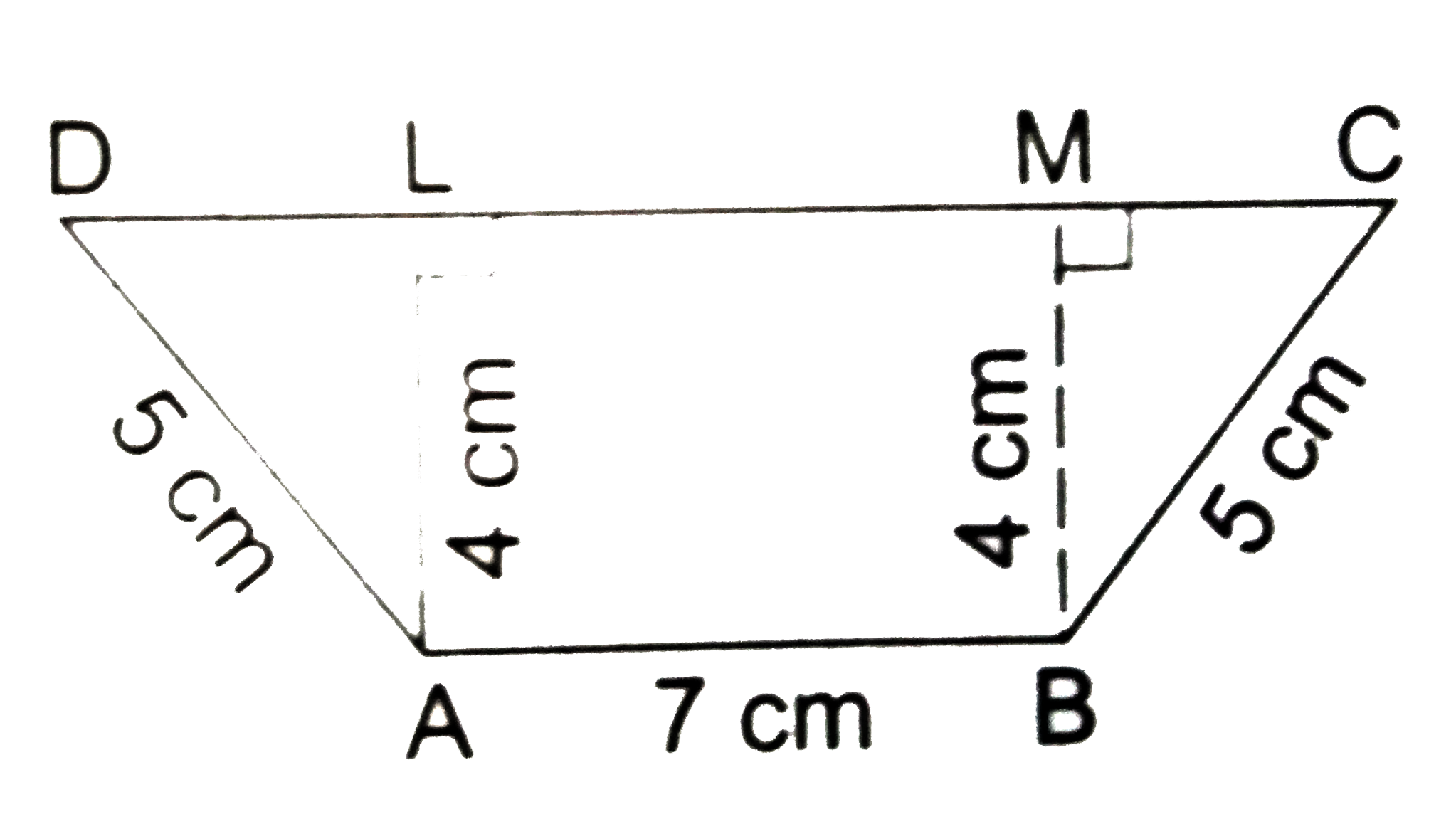
03:43View SolutionIn the given figure, ABCD is a trapezium such that AL⊥DCandBM⊥DC. If AB=7cm,BC=AD=5cm and AL=BM=4cm then ar(trap.ABCD)=?
04:36View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है तथा EFCD एक आयत है। साथ ही AL⊥DC, तो सिद्ध कीजिए कि
(i)ar(ABCD)=ar(EFCD)
(ii)ar(ABCD)=DC×AL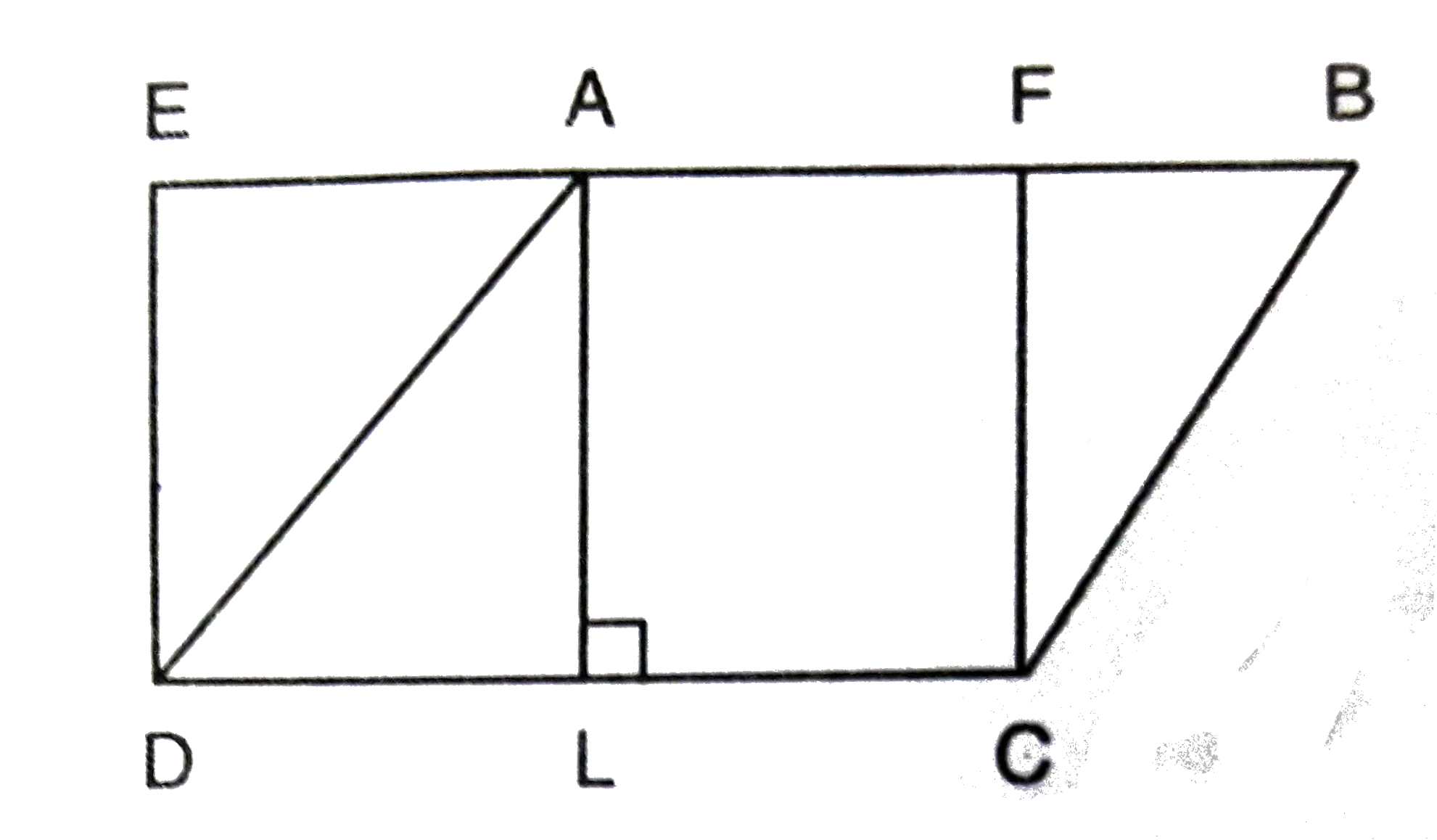
04:04View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)07:27View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG05:03View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG04:39View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG04:18View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG03:05View SolutionABCD is a trapezium whose parallel sides AB=acm And DC=bcm Is E and F is the midpoint of the parallel sides. The ratio of ar (ABFE) and ar (EFCD) is
02:56View SolutionIn Fig.
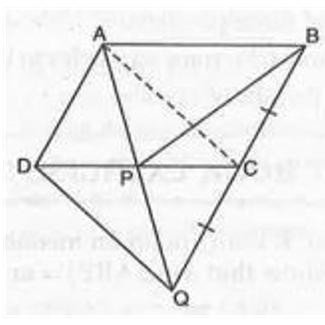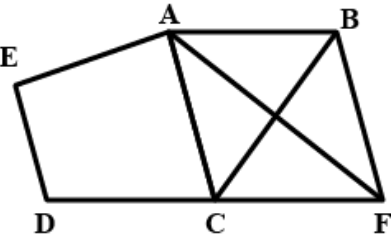
ABCD is a parallelogram. Prove that ar (ΔBCP) = ar (ΔDPQ).05:11View SolutionIn Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:- (i) ar (ACB) = ar (ACF) (ii) ar (AEDF) = ar (ABCDE)
01:35View Solution