In Fig.
 ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX⊥DE meets BC at Y. Show that : ar(BCED)=ar(ABMN)+ar(ACFG).Solution in Punjabi
ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX⊥DE meets BC at Y. Show that : ar(BCED)=ar(ABMN)+ar(ACFG).Solution in Punjabi
Step by step video & image solution for In Fig. ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX _|_ DE meets BC at Y. Show that : ar(BCED)=ar(ABMN)+ar(ACFG). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
I travelled 432 km by car and 48 litres of the petrol was consumed. I have to go at a place which is 180 km far. How much litres of the petrol is needed for it ?
View SolutionThe centre of a circle lies in .............. of the circle.
View Solutionदी गए आकृति में ABC एक समकोण त्रिभुज है जिसके कोण A समकोण है | BCED,ACFG और ABMN क्रमशः भुजाओं BC ,CA और AB पर बने वर्ग है| रेखाखण्ड AX⊥DE भुजा BC से बिंदु Y पर मिलता हैं |दर्शाइए की :
(i)ΔMBC≡ΔABD
(ii)ar(BYXD)=2ar(MBC)
(iii)ar(BYXD)=ar(ABMN)
(iv) ΔFCB=ΔACE
(v)ar(CYXE)=2ar(FCB)
(vi)ar(CYXE)=ar(ACFG)
(vii)ar(BCED)=ar(ABMN)+ar(ACFG)
(viii)BC2=AB2+AC2
(##KCSHINMATIXC11SLV032_Q01##)
View SolutionIn the following figure , ABC is a right triangle right angled at A. BCED ACFG and ABMN and squares on the sides BC, CA and AB respectively , Line segement AX ⊥ DE meets BC at Y. Show that
(i) ti⟩MBC=ti⟩(MBC)
(ii) ar (BXYD) = 2 ar (MBC)
(iii) ar (BYXD) = ar(ABMN)
(iv) ti⟩FCB=ti⟩ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE ) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
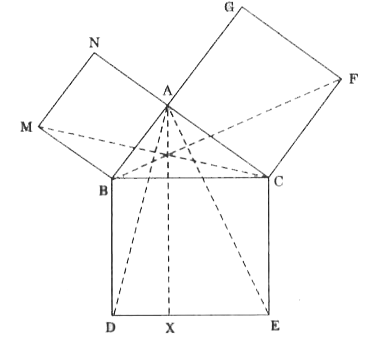
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB espectively. Line segments AX bot DE meets BC at Y. and DE at X. Join AD, AE also BF and CM (See the figure). Show that (i) DeltaMBC ~=DeltaABD
View Solutionਚਿੱਤਰ 9.34 ਵਿੱਚ, ABC ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ, ਜਿਸਦਾ ਕੋਣ A ਸਮਕੋਣ ਹੈ। BCED, ACFG ਅਤੇ ABMN ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ BC, CA ਅਤੇ AB ਉੱਤੇ ਬਣੇ ਵਰਗ ਹਨ। ਰੇਖਾ ਖੰਡ AX⊥DE ਭੁਜਾ ਨੂੰ ਬਿੰਦੂ Y 'ਤੇ ਮਿਲਦਾ ਹੈ। ਕਿ: △MBC≅△ABD
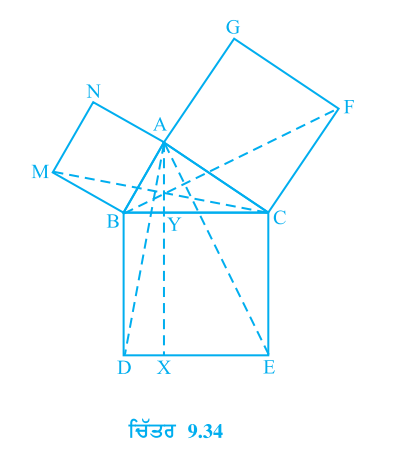
View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BYXD) =2 ar (MBC)
View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BYXD) = ar (ABMN)
View SolutionIn shape, ABC There is a right angled triangle whose angle A is right angled. BCED,ACFG And ABMN sides respectively BC, CA And AB There are classes built on. Line segment AX_|_DE arm BC meets at point Y. Show that: ar (BCED) =ar (ABMN) + ar (ACFG)
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: triangleMBC congtriangleABD
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(BYXD) =2ar(MBC)
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(BYXD) = ar(ABMN)
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: triangleFCB congtriangleACE
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(CYXE) = 2ar(FCB)
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(CYXE) = ar(ACFG)
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segent AX bot DE meets BC at Y. Show that: ar(BCED) = ar(ABMN) + ar (ACFG)
View Solution
