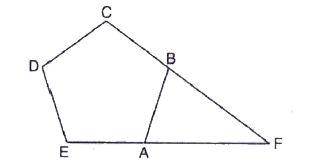
A regular pentagon ABCDE and a square ABFG are formed on opposite sides of AB. Find ∠BCF.
To find the angle ∠BCF in the given configuration of a regular pentagon ABCDE and a square ABFG, we can follow these steps:
1. Understand the Configuration:
- We have a regular pentagon ABCDE and a square ABFG formed on opposite sides of line segment AB.
2. Determine the Angles of the Pentagon:
- A regular pentagon has 5 equal angles. The sum of the interior angles of a pentagon is given by the formula:
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a pentagon, n=5:
Sum=(5−2)×180=3×180=540∘
- Therefore, each angle in a regular pentagon is:
Each angle=540∘5=108∘
3. Identify the Angles in the Square:
- Each angle in a square is 90∘.
4. Calculate ∠ABC:
- In triangle ABF, ∠ABF=90∘ (from the square) and ∠ABC=108∘ (from the pentagon).
5. Calculate ∠FBC:
- The angle ∠FBC can be found using the fact that the sum of angles around point B is 360∘:
∠FBC=360∘−∠ABF−∠ABC
- Substituting the values:
∠FBC=360∘−90∘−108∘=162∘
6. Determine ∠BCF:
- Triangle BCF is isosceles because BF=BC (both are sides of the square and pentagon respectively).
- Therefore, the angles at B and C are equal:
∠BCF=∠BFC
- The sum of angles in triangle BCF is 180∘:
∠BCF+∠BFC+∠FBC=180∘
- Let ∠BCF=x:
x+x+162∘=180∘
2x=180∘−162∘=18∘
x=18∘2=9∘
Thus, the angle ∠BCF is 9∘.
- We have a regular pentagon ABCDE and a square ABFG formed on opposite sides of line segment AB.
- A regular pentagon has 5 equal angles. The sum of the interior angles of a pentagon is given by the formula:
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a pentagon, n=5:
Sum=(5−2)×180=3×180=540∘
- Therefore, each angle in a regular pentagon is:
Each angle=540∘5=108∘
- Each angle in a square is 90∘.
- In triangle ABF, ∠ABF=90∘ (from the square) and ∠ABC=108∘ (from the pentagon).
- The angle ∠FBC can be found using the fact that the sum of angles around point B is 360∘:
∠FBC=360∘−∠ABF−∠ABC
- Substituting the values:
∠FBC=360∘−90∘−108∘=162∘
- Triangle BCF is isosceles because BF=BC (both are sides of the square and pentagon respectively).
- Therefore, the angles at B and C are equal:
∠BCF=∠BFC
- The sum of angles in triangle BCF is 180∘:
∠BCF+∠BFC+∠FBC=180∘
- Let ∠BCF=x:
x+x+162∘=180∘
2x=180∘−162∘=18∘
x=18∘2=9∘
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - APPLICATIONS, GAMES AND PUZZLES
3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
Similar Questions
Knowledge Check
ABCDE is a regular pentagon. CBF and EAF are straight lines. What kind of triangle is triangle ABF?
 ARightBEquilateralCIsoscelesDNone of these
ARightBEquilateralCIsoscelesDNone of theseIn a regular pentagon the side measures 6 cm and sum of the inradius and circumradius is 9cm. Ratio of inradius and circumradius is 1:2 respectively. Find the sum of the area of the circumcircle and the area of the incircle of the pentagon.
A41πcm2B45πcm2C53πcm2Ddata insufficientABCDE is a regular pentagon. Angle bisector of ∠BAE meets CD at m. angle bisector of ∠BCD meets AM at P. Find the ∠CPM= ?
A30B35C36D60
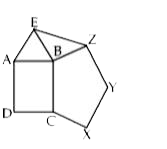
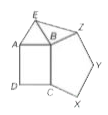
In the given figure , ABCD is a square BCXYZ is a regular pentagon and ABE is an equilateral triangle . What is the value (in degrees) of ∠EBZ ?
View SolutionABCD is a square. Find out the side of square?
View SolutionABCDE is a regular pentagon. Its sides are extended as shown in the figure. The value of ∠ABC+2∠EGD+3∠BAJ6 is:

View SolutionA wire of length 20 is cut into two parts one is made into regular hexagon of side a and other to square . Find a if combined area of square and regular hexagon is minimum
View SolutionFind the perimeter of
(i) a regular pentagon of side 8 cm.
(ii) a regular octagon of side 4.5 cm.
(iii) a regular decagon of side 3.6 cm.
View Solution