In △PQR, QT is perpendicular to PR and s is a point on QR such that, ∠PSQ=p∘. If ∠TQR=46∘ and ∠SPR=32∘, then the value of p is :
त्रिभुज
PQR में, QT, PR पर लंब है और QR पर बिंदु s इस प्रकार पर है कि ∠PSQ=p∘ है| यदि ∠TQR=46∘ और ∠SPR=32∘ है, तो p का मान ज्ञात करें|
78∘
82∘
76∘
72∘
To solve the problem, we will follow these steps:
Step 1: Understand the triangle and given angles
We have triangle PQR with QT perpendicular to PR. We know:
- ∠TQR=46∘
- ∠SPR=32∘
Step 2: Find ∠QRT
In triangle QTR, we can use the fact that the sum of angles in a triangle is 180∘. Thus, we can write:
∠QRT+∠TQR+∠QTR=180∘
Substituting the known values:
∠QRT+46∘+90∘=180∘
∠QRT+136∘=180∘
∠QRT=180∘−136∘=44∘
Step 3: Find ∠PSR
Now we will consider triangle PSR. The angles in triangle PSR are:
∠PSR+∠SPR+∠QRT=180∘
Substituting the known values:
∠PSR+32∘+44∘=180∘
∠PSR+76∘=180∘
∠PSR=180∘−76∘=104∘
Step 4: Find ∠PSQ
Now, we know that:
∠PSQ+∠PSR+∠QSR=180∘
Since QR is a straight line, we have:
∠PSQ+∠PSR+∠QSR=180∘
We can express ∠QSR as:
∠QSR=180∘−∠PSR
Substituting the known values:
∠PSQ+104∘+∠QSR=180∘
Since ∠QSR=180∘−∠PSR:
∠PSQ+104∘+(180∘−104∘)=180∘
This simplifies to:
∠PSQ+180∘=180∘
Thus:
∠PSQ=180∘−104∘=76∘
Conclusion
The value of p is:
p=76∘
We have triangle PQR with QT perpendicular to PR. We know:
- ∠TQR=46∘
- ∠SPR=32∘
In triangle QTR, we can use the fact that the sum of angles in a triangle is 180∘. Thus, we can write:
∠QRT+∠TQR+∠QTR=180∘
Substituting the known values:
∠QRT+46∘+90∘=180∘
∠QRT+136∘=180∘
∠QRT=180∘−136∘=44∘
Now we will consider triangle PSR. The angles in triangle PSR are:
∠PSR+∠SPR+∠QRT=180∘
Substituting the known values:
∠PSR+32∘+44∘=180∘
∠PSR+76∘=180∘
∠PSR=180∘−76∘=104∘
Now, we know that:
∠PSQ+∠PSR+∠QSR=180∘
Since QR is a straight line, we have:
∠PSQ+∠PSR+∠QSR=180∘
We can express ∠QSR as:
∠QSR=180∘−∠PSR
Substituting the known values:
∠PSQ+104∘+∠QSR=180∘
Since ∠QSR=180∘−∠PSR:
∠PSQ+104∘+(180∘−104∘)=180∘
This simplifies to:
∠PSQ+180∘=180∘
Thus:
∠PSQ=180∘−104∘=76∘
The value of p is:
p=76∘
Topper's Solved these Questions
Similar Questions
In △ABC,BD⊥AC, at D, E is a point on BC such that ∠BEA=x∘,If ∠EAC=46∘ and ∠EBD=60∘, then the value of x is:
त्रिभुज ABC में, BD⊥AC, E, BC पर एक बिंदु इस प्रकार है की ∠BEA=x∘ , यदि ∠EAC=46∘ और ∠EBD=60∘, तो x का मान ज्ञात करे |
View SolutionIn △ABC ,BD is perpendicular to AC. E is a point on BC such that ∠BEA=x∘. If ∠EAC=38∘ and ∠EBD=40∘, then the value of x is:
त्रिभुज ABC में,BD, AC पर लम्ब है | E, BC पर स्थित ऐसा बिंदु है कि ∠BEA=x∘ है | यदि ∠EAC=38∘ और ∠EBD=40∘ है, तो x का मान क्या होगा ?
View Solution
Knowledge Check
In figure, if QT⊥PR,∠TQR=40∘and∠SPR=30∘, find value of y-x
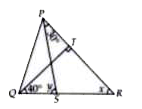 A80∘B50∘C30∘D130∘
A80∘B50∘C30∘D130∘In ΔPQT,PQ=PT. The points R and S are on QT such that PR = PS. If ∠PTS=62∘and∠RPS=34∘, then measure of ∠QPR is
A11∘B13∘C15∘D17∘In ΔPQT,PQ=PT . The points R and S are on QT such that PR = PS . If ∠PTS=62∘and∠RPS=34∘ then measure of ∠QPR is
A11∘B13∘C15∘D17∘
In ΔPQR, S is a point in QR such that angle PQS= angle SPR show that angle PSR= angle QPR
View SolutionIn △ABC,BD⊥AC, at D,E is a point on BC such that ∠BEA=x∘. If ∠EAC=62∘ and ∠EBD=60∘, then the value of x is :
त्रिभुज ABC में, BD⊥AC पर D, E, BC पर एक बिंदु है जेसे कि ∠BEA=x∘ यदि ∠EAC=62∘ और ∠EBD=60∘ है, तो x का मान है :
View SolutionIn △ABC ,AD is perpendicular to BC at D and AE is the bisector of angle A. If ∠B=72∘ and ∠C=26∘ then what is the measure of ∠DAE ?
त्रिभुज ABC में, AD, BC पर लम्ब है जो D पर डाला गया है तथा AE कोण A का द्विभाजक है | यदि ∠B=72∘ and ∠C=26∘ है, तो कोण DAE का मान ज्ञात करें |
View SolutionIn △PQR,∠Q≻∠R, PS is the bisector of ∠P and PT⊥QR. If ∠SPT=28∘ and ∠R=23∘ , then the measure of ∠Q is:
त्रिभुज PQR में, ∠Q≻∠R, है तथा PS कोण P का समद्विभाजक है और PT⊥QR है । यदि ∠SPT=28∘ और ∠R=23∘ है, तो कोण Q का मान क्या है?
View SolutionIn △ABC ,D is a point on BC such that ∠BAD=12∠ADC, ∠BAC=87∘ and ∠C=42∘. What is the measure of ∠ADB ?
त्रिभुज ABC में, D, BC पर स्थित एक बिंदु है जो इस प्रकार है कि 2∠BAD=12∠ADC, ∠BAC=87∘ तथा ∠C=42∘ है | कोण ADB का माप क्या होगा ?
View Solution
