From a point P , outside a circle, PAB is a secant and PT is a tangent to the circle, where A , B and T are points on the circle. If PT = 5cm , PA = 4cm and AB = x , then x is equal to:
वृत्त के बाहर एक बिंदु P से , PAB एक छेदक रेखा तथा PT वृत्त की एक स्पर्श रेखा है एवं A, B और T वृत्त पर स्थित बिंदु हैं | यदि PT=5 सेमी, PA = 4 सेमी तथा AB = x सेमी है, तो x का मान किसके बराबर होगा ?
2.25
2.75
2.45
1.75
To solve the problem, we will use the property of circles that relates the lengths of the tangent and secant segments. The property states that the square of the length of the tangent segment from a point outside the circle is equal to the product of the lengths of the entire secant segment and its external segment.
1. Identify Given Values:
- Length of the tangent PT=5cm
- Length of the segment from point P to point A (external segment) PA=4cm
- Length of the segment AB=xcm
2. Use the Circle Tangent-Secant Theorem:
According to the theorem:
PT2=PA×PB
where PB is the entire secant segment from point P to point B.
3. Express PB in terms of x:
Since PB consists of PA and AB, we can express it as:
PB=PA+AB=4+x
4. Substitute Values into the Equation:
Now substituting the known values into the equation:
PT2=PA×PB
becomes:
52=4×(4+x)
Simplifying this gives:
25=4×(4+x)
5. Distribute and Rearrange the Equation:
Expanding the right side:
25=16+4x
Now, rearranging the equation to isolate x:
25−16=4x
9=4x
6. Solve for x:
Dividing both sides by 4:
x=94=2.25cm
Final Answer:
Thus, the value of x is 2.25cm.
---
- Length of the tangent PT=5cm
- Length of the segment from point P to point A (external segment) PA=4cm
- Length of the segment AB=xcm
According to the theorem:
PT2=PA×PB
where PB is the entire secant segment from point P to point B.
Since PB consists of PA and AB, we can express it as:
PB=PA+AB=4+x
Now substituting the known values into the equation:
PT2=PA×PB
becomes:
52=4×(4+x)
Simplifying this gives:
25=4×(4+x)
Expanding the right side:
25=16+4x
Now, rearranging the equation to isolate x:
25−16=4x
9=4x
Dividing both sides by 4:
x=94=2.25cm
Thus, the value of x is 2.25cm.
Topper's Solved these Questions
Similar Questions
Chord AB of a circle is produced to a point P, and C is a point on the circle such that PC is a tangent to the circle. If PC=18 cm, and BP = 15 cm, then AB is equal to :
किसी वृत्त की जीवा AB को एक बिंदु P तक बढ़ाया जाता है तथा C वृत्त पर स्थित एक ऐसा बिंदु है कि PC वृत्त की एक स्पर्श रेखा है | यदि PC = 18 सेमी और BP = 15 सेमी है, तो AB का मान किसके बराबर है ?
View SolutionPA and PB are two tangents from a point P outside the circle with centre O. If A and B are points on the circle such that ∠APB=40∘, then ∠OAB is equal to:
PA तथा PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | A तथा B वृत्त पर स्थित बिंदु हैं |यदि ∠APB=40∘ है, तो ∠OAB किसके बराबर है ?
View Solution
Knowledge Check
In the figure, PT = 5 cm, PA = 4 cm. Find AB
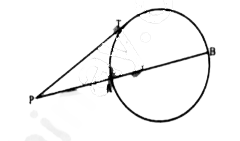 A49cmB94cmC5cmD23cm
A49cmB94cmC5cmD23cm
Two chords AB and CD of a circle intersect at a point P inside the circle. If AB = 7cm , PC = 2 cm and AP = 4 cm, then CD is equal to:
एक वृत्त की दो जीवाएं AB और CD वृत्त के भीतर बिंदु P पर एक दूसरे को काटती हैं | यदि AB = 7 सेमी, PC = 2 सेमी और AP = 4 सेमी है, तो CD किसके बराबर होगा ?
View SolutionTwo chords AB and CD of a circle, when produced, meet at a point P outside the circle. If AB = 6 cm , PB = 5 cm , PD = 4 cm, then CD is equal to :
एक वृत्त की दो जीवाओं AB और CD को जब बढ़ाया जाता है तो वे वृत्त के बाहर बिंदु P पर मिलती हैं | यदि AB=6 सेमी, PB = 5 सेमी और PD = 4 सेमी है, तो CD का मान किसके बराबर है ?
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle, and A and B are points on the circle. If ∠APB=40∘, then ∠OAB is equal to:
PA तथा PB एक वृत्त के बाहर स्थित बिंदु P से वृत्त की स्पर्श रेखाएं हैं जिसका केंद्र O है तथा A और B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=40∘ है, तो ∠OAB का मान ज्ञात करें |
View SolutionPA and PB are two tangents from a point P outside the circle with centre O. If A and B are points on the circle such that ∠APB=110∘, then ∠OAB is equal to:
PA तथा PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे बिंदु हैं कि ∠APB=110∘ है, तो ∠OAB किसके बराबर है ?
View SolutionPA and PB are two tangents from a point P outside the circle with centre O. If A and B are points on the circle such that ∠APB=130∘, then ∠OAB is equal to:
PA तथा PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे बिंदु हैं कि ∠APB=130∘ है, तो ∠OAB किसके बराबर है ?
View SolutionChords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm. AP = 4 cm and PC = 5 cm, then CD is equal to:
एक वृत्त की जीवायें AB और CD वृत्त के भीतर स्थित बिंदु P पर एक दूसरे को काटती हैं | यदि AB =10 सेमी,AP = 4 सेमी और PC = 5 सेमी है, तो CD का मान क्या होगा ?
View SolutionIn the following figure, PR is a secant and PT is a tangent to the circle. If PT=6cm and QR=5cm , then PQ= _______cm.
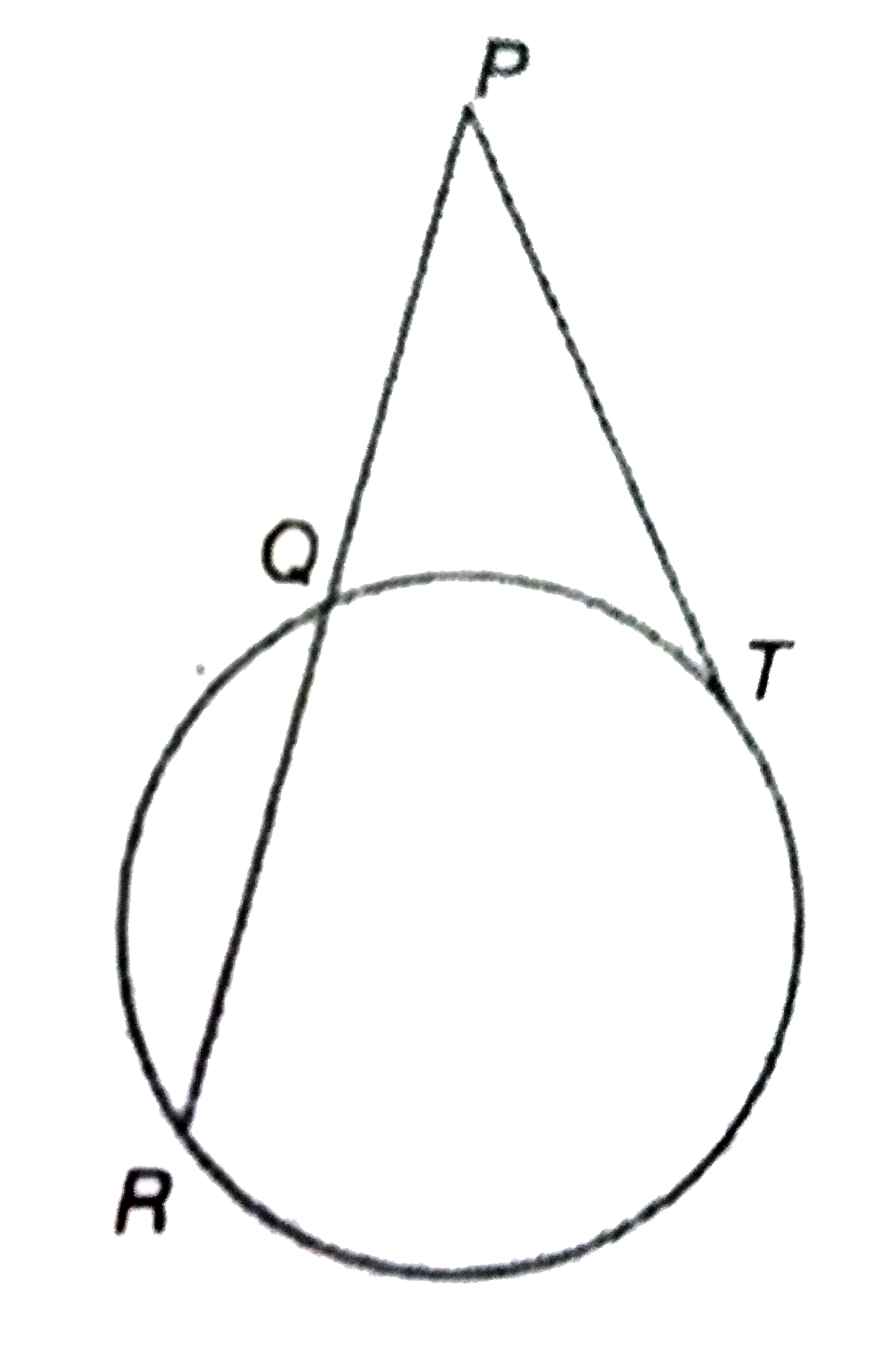
View Solution