In a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=24∘ , then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=24∘ है, तो ∠CAD का मान ज्ञात करें |
24
42
36
48
To solve the problem step by step, we will follow the properties of circles and trapeziums.
Step 1: Understand the Given Information
We have a circle with center O, where AB is the diameter, and CD is a chord such that ABCD forms a trapezium. We are given that angle BAC = 24°.
Step 2: Draw the Circle and Label Points
Draw a circle with center O. Mark points A and B on the circle such that AB is the diameter. Now, draw a chord CD such that ABCD forms a trapezium. Label the points as follows:
- A (on the left end of the diameter)
- B (on the right end of the diameter)
- C (on the upper part of the chord)
- D (on the upper part of the chord)
Step 3: Identify Angles
We know that angle BAC = 24°. We need to find angle CAD. Let's denote angle CAD as X.
Step 4: Use Properties of Trapezium
Since ABCD is a trapezium, we know that AB is parallel to CD. By the properties of parallel lines, we can say that angle BAC (24°) will be equal to angle CAD (X) because they are alternate interior angles.
Step 5: Establish Relationships of Angles
Since angle BAC = 24°, we can conclude that angle CAD = angle BCA = 24° (by the alternate interior angles property).
Step 6: Use the Circle Theorem
In any circle, the angles subtended by the same arc at the circumference are equal. Therefore, if arc AD subtends angle B at point C, it will also subtend the same angle at point D.
Step 7: Analyze Triangle ADB
Now, we will analyze triangle ADB. The angles in triangle ADB should sum up to 180°:
- Angle ADB = 90° (since AB is the diameter)
- Angle BAC = 24°
- Angle CAD = X
So, we can write the equation:
90°+24°+X=180°
Step 8: Solve for X
Now, let's solve for X:
1. Combine the known angles:
90°+24°=114°
2. Substitute back into the equation:
114°+X=180°
3. Isolate X:
X=180°−114°
X=66°
Final Answer
Thus, angle CAD is equal to 66°.
---
We have a circle with center O, where AB is the diameter, and CD is a chord such that ABCD forms a trapezium. We are given that angle BAC = 24°.
Draw a circle with center O. Mark points A and B on the circle such that AB is the diameter. Now, draw a chord CD such that ABCD forms a trapezium. Label the points as follows:
- A (on the left end of the diameter)
- B (on the right end of the diameter)
- C (on the upper part of the chord)
- D (on the upper part of the chord)
We know that angle BAC = 24°. We need to find angle CAD. Let's denote angle CAD as X.
Since ABCD is a trapezium, we know that AB is parallel to CD. By the properties of parallel lines, we can say that angle BAC (24°) will be equal to angle CAD (X) because they are alternate interior angles.
Since angle BAC = 24°, we can conclude that angle CAD = angle BCA = 24° (by the alternate interior angles property).
In any circle, the angles subtended by the same arc at the circumference are equal. Therefore, if arc AD subtends angle B at point C, it will also subtend the same angle at point D.
Now, we will analyze triangle ADB. The angles in triangle ADB should sum up to 180°:
- Angle ADB = 90° (since AB is the diameter)
- Angle BAC = 24°
- Angle CAD = X
90°+24°+X=180°
Now, let's solve for X:
1. Combine the known angles:
90°+24°=114°
2. Substitute back into the equation:
114°+X=180°
3. Isolate X:
X=180°−114°
X=66°
Thus, angle CAD is equal to 66°.
Topper's Solved these Questions
Similar Questions
In a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=25∘ , then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=25∘ है, तो ∠CAD का मान ज्ञात करें |
View SolutionIn a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=18∘, then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=18∘ है, तो ∠CAD का मान ज्ञात करें |
View SolutionIn a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=40∘., then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है और CD एक ऐसी जीवा है कि ABCD समलम्ब है | यदि ∠BAC=40∘ है, तो ∠CAD ज्ञात करें|
View SolutionIn a circle with centre O, AB is a diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=28∘ ,then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB एक व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब है | यदि ∠BAC=28∘ , है, तो कोण CAD ज्ञात करें |
View SolutionIn a circle with centre O, AD is a diameter and AC is a chord. Point B on AC such that OB = 7cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र वाले एक वृत्त में, AD एक व्यास है और AC एक जीवा है। AC पर एक बिंदु B इस प्रकार है की OB = 7 सेमी और ∠OBA=60∘ | यदि ∠DOC=60∘ है, तो BC की लंबाई क्या है?
View SolutionIn a circle with centre O, AD is a diameter and AC is a chord. B is a point on AC, such that OB = 5 cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र O वाले एक वृत्त में, AD व्यास है तथा AC जीवा है | B, AC पर स्थित बिंदु है जो इस प्रकार है कि OB =5 सेमी तथा ∠OBA=60∘ है | यदि ∠DOC=60∘ है, तो BC की लंबाई ज्ञात करें |
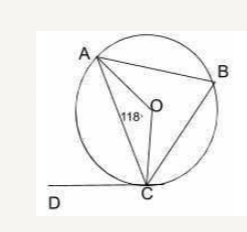
View SolutionIn the given figure, BC is a chord and CD is a tangent through the point C. If ∠AOC=118∘, then find the ∠ACD.
दी गयी आकृति में, BC एक जीवा है तथा CD एक स्पर्श रेखा है जो C से जाती है। यदि ∠AOC=118∘ है, तो ∠ACD का मान ज्ञात कीजिए।
View SolutionAB is a diameter of a circle with centre O, and P is a point on the circle. If ∠POA=130∘, the ∠PBO is equal to:
AB केंद्र O के साथ एक वृत्त पर एक व्यास है, और P वृत्त का एक बिंदु है। यदि ∠POA=130∘, तो ∠PBO का मान ज्ञात करे|
View SolutionThe tangent at a point A of a circle with centre O intersects the diameter PQ of the circle (when extended) at the point B. If ∠BAP=125∘, then ∠AQP is equal to:
केंद्र O के साथ एक वृत्त के बिंदु A पर स्पश्रेखा, बिंदु , B पर वृत्त के व्यास PQ ( जब विस्तारित) को काटती है यदि∠BAP=125∘ है, तो ∠AQP के ज्ञात करें ।
View SolutionIn a circle with centre O, A diameter AB and a chord CD intersect each other at E, Ac and AD are joined. If ∠BOC=48∘ and ∠AOD=100∘, then what is the measure of ∠CEB ?
केंद्र O वाले एक वृत्त में, व्यास AB तथा जीवा CD एक दूसरे को E पर काटते हैं | AC तथा AD को मिलाया जाता है | यदि ∠BOC=48∘ है और ∠AOD=100∘ है, तो ∠CEB का मान ज्ञात करें |
View Solution