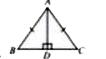
In the given figure, △ A B C is an isosceles triangle, in which AB=AC, A D ⊥ B C , BC = 6cm and AD = 4cm. The length of AB is:
दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC, A D ⊥ B C , BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ?
In the given figure, triangle ABC is an isosceles triangle, in which AB=AC, AD bot BC, BC = 6cm and AD = 4cm. The length of AB is: दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC,AD bot BC, BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ?

A

6 cm

B

7 cm

C

4 cm

D

5 cm

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for In the given figure, triangle ABC is an isosceles triangle, in which AB=AC, AD bot BC, BC = 6cm and AD = 4cm. The length of AB is: दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC,AD bot BC, BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023
Class 14MATHSGEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In the given figure, △ABC is an isosceles triangle, in which AB=AC, AD⊥BC, BC = 6cm and AD = 4cm. The length of AB is:
    दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC,AD⊥BC, BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ?
    ocr_image

    A4 cm
    B6 cm
    C7 cm
    D5 cm

  • ΔABC is an isosceles triangles with AB = AC = 10 cm,AD =8 cm M is the median on BC from A. The length of BC is

    A8 cm
    B12 cm
    C10 cm
    D6 cm

  • In △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :

    A√3172cm
    B√1192cm
    C√1152cm
    D√3132cm