A, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 80∘ and 120∘, respectively. The value of ∠BAC is:
A, B तथा C एक वृत्त पर स्थित तीन
ऐसे बिंदु हैं कि जीवाओं AB तथा AC के द्वारा केंद्र पर अंतरित कोण क्रमशः 80∘ तथा 120∘ हैं | कोण BAC का मान क्या है ?
75∘
80∘
85∘
70∘
To solve the problem, we need to find the measure of angle BAC given the angles subtended by chords AB and AC at the center O of the circle.
1. Identify the Given Angles:
- The angle subtended by chord AB at the center O is ∠AOB=80∘.
- The angle subtended by chord AC at the center O is ∠AOC=120∘.
2. Calculate the Angle BOC:
- The sum of angles around point O must equal 360∘.
- Therefore, we can find ∠BOC using the equation:
∠AOB+∠AOC+∠BOC=360∘
- Substituting the known values:
80∘+120∘+∠BOC=360∘
- This simplifies to:
∠BOC=360∘−200∘=160∘
3. Use the Inscribed Angle Theorem:
- According to the inscribed angle theorem, the angle subtended by an arc at the center is twice the angle subtended by the same arc at any point on the circle.
- Therefore, we have:
∠BAC=12∠BOC
- Substituting the value of ∠BOC:
∠BAC=12×160∘=80∘
4. Conclusion:
- The value of angle BAC is 80∘.
Final Answer:
∠BAC=80∘
- The angle subtended by chord AB at the center O is ∠AOB=80∘.
- The angle subtended by chord AC at the center O is ∠AOC=120∘.
- The sum of angles around point O must equal 360∘.
- Therefore, we can find ∠BOC using the equation:
∠AOB+∠AOC+∠BOC=360∘
- Substituting the known values:
80∘+120∘+∠BOC=360∘
- This simplifies to:
∠BOC=360∘−200∘=160∘
- According to the inscribed angle theorem, the angle subtended by an arc at the center is twice the angle subtended by the same arc at any point on the circle.
- Therefore, we have:
∠BAC=12∠BOC
- Substituting the value of ∠BOC:
∠BAC=12×160∘=80∘
- The value of angle BAC is 80∘.
∠BAC=80∘
Topper's Solved these Questions
Similar Questions
A,B and C are three points on a circle such that the angles subtended by the chord AB and AC at the centre O are 110∘ and 130∘ respectively. Then the value of ∠BAC is:
A, B और C एक वृत्त पर स्थित तीन ऐसे बिंदु हैं कि जीवा AB और AC के द्वारा केंद्र O पर अंतरित किये गए कोण क्रमशः 110∘ तथा 130∘ हैं| ∠BAC का मान है :
View SolutionA,BandC are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90∘a n d 110∘, respectively. Determine ∠BAC
View Solution
Knowledge Check
A, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 80∘ and 120∘, respectively. The value of ∠BAC is:
A, B तथा C एक वृत्त पर स्थित तीन ऐसे बिंदु हैं कि जीवाओं AB तथा AC के द्वारा केंद्र पर अंतरित कोण क्रमशः 80∘ तथा 120∘ हैं | कोण BAC का मान क्या है ?A85∘B75∘C80∘D70∘A, B and C are three points on a circle such that the angles subtended by the chord AB and AC at the centre O are 110° and 130°, respectively. The value of ∠BAC is:
A75∘B70∘C60∘D65∘A, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 110°∘and 130∘ respectively. Then the value of ∠BAC is :
A75∘B70∘C60∘D65∘
In Figure, A,B,C are three points on a circle such that the angles sub center O are 80∘and120∘ respectively. Determine ∠BAC and the degree measure of arc BPC
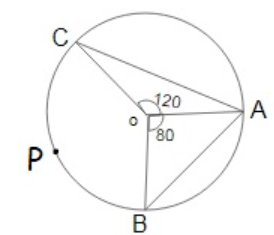
View SolutionA, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 80∘ and 120∘, respectively. The value of ∠BAC is:
A, B तथा C एक वृत्त पर स्थित तीन ऐसे बिंदु हैं कि जीवाओं AB तथा AC के द्वारा केंद्र पर अंतरित कोण क्रमशः 80∘ तथा 120∘ हैं | कोण BAC का मान क्या है ?
View SolutionA, B and C are the three points on a circle such that the angle subtendsed by the chords AB and AC at the centre O are 90∘ and 110∘ respectively. ∠BAC is equal to
View SolutionA,B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90∘ and 110∘ respectively . Further suppose that the centre O lies on the interior ∠BAC. The ∠BAC is
View SolutionA,B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90∘ and 110∘ respectively . Further suppose that the centre O lies on the interior ∠BAC. The ∠BAC is
View Solution
