Two tangents AP and AQ are drawn to a circle with centre O from an external point A, where P and Q are points on the circle. If AP = 12 cm and ∠PAQ=60∘, then the length of chord PQ is:
दो स्पर्शरेखा AP और AQ एक बाहरी बिंदु A से क O के साथ वृत्त में खींचे जाते हैं,,जहां P और Q वृत्त पर स्थित बिंदु हैं। यदि AP = 12 cm और ∠PAQ=60∘, तब जीवाएँ PQ की लंबाई हैं :
12 cm
10 cm
24 cm
16 cm
To find the length of the chord PQ given the tangents AP and AQ from point A to the circle with center O, we can follow these steps:
Step 1: Understand the Geometry
We have two tangents AP and AQ from point A to the circle, where P and Q are the points of tangency. The lengths of the tangents from a point outside the circle to the points of tangency are equal. Therefore, AP = AQ = 12 cm.
Step 2: Analyze the Angle
We are given that the angle ∠PAQ = 60°. Since AP and AQ are tangents, the angles ∠OAP and ∠OAQ are both right angles (90°).
Step 3: Use Triangle Properties
In triangle OAP:
- ∠OAP = 90°
- ∠PAQ = 60°
- Therefore, ∠OAP + ∠PAQ + ∠OAP = 180°
- This implies that ∠APO = ∠AQP = 30° (since the triangle is isosceles with AP = AQ).
Step 4: Apply the 30-60-90 Triangle Ratios
In triangle OAP:
- The sides opposite the angles are in the ratio 1:√3:2.
- Let OP = x (the radius of the circle), OA = 12 cm (the length of the tangent), and AP = 12 cm.
From the 30-60-90 triangle properties:
- The side opposite the 30° angle (OP) is half the hypotenuse (OA).
- Therefore, OA = 2 * OP.
Step 5: Calculate OP
Using the tangent length:
- OA = AP = 12 cm.
- Since OA = 2 * OP, we have:
OP=OA2=122=6 cm
Step 6: Find the Length of Chord PQ
Now, we can find the length of the chord PQ using the formula for the length of the chord in terms of the radius and the angle subtended at the center:
- The angle ∠POQ = 2 * ∠PAQ = 2 * 60° = 120°.
- The length of chord PQ can be calculated using the formula:
PQ=2∗OP∗sin(∠POQ2)
PQ=2∗6∗sin(60°)
PQ=12∗√32=6√3 cm
Step 7: Final Calculation
To find the numerical value of 6√3:
- Using √3≈1.732:
PQ≈6∗1.732≈10.392 cm
Thus, the length of chord PQ is approximately 10.39 cm.
Summary of Steps:
1. Identify the geometry and angles.
2. Use triangle properties to find the radius.
3. Apply the chord length formula.
We have two tangents AP and AQ from point A to the circle, where P and Q are the points of tangency. The lengths of the tangents from a point outside the circle to the points of tangency are equal. Therefore, AP = AQ = 12 cm.
We are given that the angle ∠PAQ = 60°. Since AP and AQ are tangents, the angles ∠OAP and ∠OAQ are both right angles (90°).
In triangle OAP:
- ∠OAP = 90°
- ∠PAQ = 60°
- Therefore, ∠OAP + ∠PAQ + ∠OAP = 180°
- This implies that ∠APO = ∠AQP = 30° (since the triangle is isosceles with AP = AQ).
In triangle OAP:
- The sides opposite the angles are in the ratio 1:√3:2.
- Let OP = x (the radius of the circle), OA = 12 cm (the length of the tangent), and AP = 12 cm.
- The side opposite the 30° angle (OP) is half the hypotenuse (OA).
- Therefore, OA = 2 * OP.
Using the tangent length:
- OA = AP = 12 cm.
- Since OA = 2 * OP, we have:
OP=OA2=122=6 cm
Now, we can find the length of the chord PQ using the formula for the length of the chord in terms of the radius and the angle subtended at the center:
- The angle ∠POQ = 2 * ∠PAQ = 2 * 60° = 120°.
- The length of chord PQ can be calculated using the formula:
PQ=2∗OP∗sin(∠POQ2)
PQ=2∗6∗sin(60°)
PQ=12∗√32=6√3 cm
To find the numerical value of 6√3:
- Using √3≈1.732:
PQ≈6∗1.732≈10.392 cm
1. Identify the geometry and angles.
2. Use triangle properties to find the radius.
3. Apply the chord length formula.
Topper's Solved these Questions
Similar Questions
Two tangents AP and AQ are drawn to a circle with centre O from an external point A, where P and Q are points on the circle. If the ∠PAQ=70∘, then the ∠AOP is equal to:
दो स्पर्शरेखा AP और AQ एक बाहरी बिंदु A से केंद्र O के साथ एक वृत्त में खींची जाती हैं, जहां P और Q वृत्त पर बिंदु होते हैं। यदि ∠PAQ=70∘, तो ∠AOP का मान है:
View SolutionIn From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
View Solution
Knowledge Check
To a circle with centre at 0, two tangents AP and AQ are drawn from an external point A. If the ∠PAQ = 80∘, then the ∠POQ is:
A80∘B70∘C90∘D100∘
PA and PB are tangents to a circle with centre O, from a point P outside the circle, and A and B are points on the circle. If ∠APB=40∘, then ∠OAB is equal to:
PA तथा PB एक वृत्त के बाहर स्थित बिंदु P से वृत्त की स्पर्श रेखाएं हैं जिसका केंद्र O है तथा A और B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=40∘ है, तो ∠OAB का मान ज्ञात करें |
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠OAB=20∘, then ∠APB is equal to:
PA तथा PB केंद्र O वाले वृत के बाहर स्थित बिंदु P से वृत्त पर खींची गयी दो स्पर्श रेखाएं हैं | A और B वृत्त पर स्थित बिंदु हैं | यदि ∠OAB=20∘ है, तो ∠APB का मान कया होगा ?
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle A and B are points on the circle. If ∠APB=86∘, then ∠OAB is equal to:
PA तथा PB केंद्र O वाले वृत के बाहर स्थित बिंदु P से वृत्त पर खींची गयी दो स्पर्श रेखाएं हैं | A और B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=86∘ है, तो ∠OAB का ज्ञात करें |
View SolutionIn Figure, there are two concentric circles with centre O of radii 5cmand3cm . From an external point P, tangents PAandPB are drawn to these circles. If AP=12cm, find the length of BP.
View SolutionIn Fig AP and BP are tangents to a circle with centre O, such that AP = 5 cm , and ∠APB=60∘ . Find the length of chord AB.
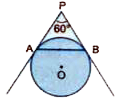
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle A and B are points on the circle. If ∠OAB=38∘, then ∠APB is equal to:
PA तथा PB केंद्र O वाले वृत के बाहर स्थित बिंदु P से वृत्त पर खींची गयी दो स्पर्श रेखाएं हैं | A और B वृत्त पर स्थित बिंदु हैं | यदि ∠OAB=38∘, है, तो ∠APB का ज्ञात करें |
View SolutionTwo tangents PA and PB are drawn from an external point P to a circle with centre O at the point A and B respectively on it, such that ∠APB=120∘, and AP= 12.5 cm. The length of OP is:
दो स्पर्शरेखाएँ PA और PB एक बाहरी बिंदु P से एक बिंदु पर क्रमशः केंद्र A और B पर O के साथ वृत्त की ओर खींची जाती हैं, जैसे कि ∠APB=120∘ और AP = 12.5 cm OP की लंबाई है:
View Solution
